ГДЗ по Алгебре 9 Класс Остальные Задания Для Старого Учебника(2019) Номер 790 Дорофеев, Суворова — Подробные Ответы

Девятиклассники отгадывали кроссворд (каждый самостоятельно). После этого они сравнили число неразгаданных слов. Данные представлены в таблице на с. 320.
а) Для каждого количества неразгаданных слов составьте таблицу частот.
б) Постройте полигон частот.
в) Найдите процент ребят, не разгадавших более двух слов.
г) Найдите среднее число неразгаданных слов в кроссворде.

а) Таблица частот количества неразгаданных слов:

$S = 3 + 6 + 6 + 3 = 18;$

$v_1 = v_4 = \frac{3}{18} \approx 0,17;$

$v_2 = v_3 = \frac{6}{18} \approx 0,33;$

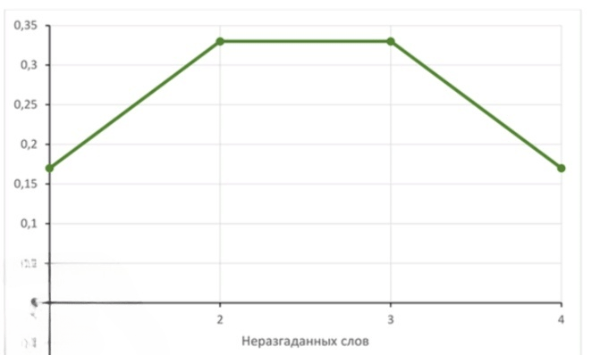
б) Полигон частот:

в) Процент ребят, не разгадавших более двух слов: $\frac{6 + 3}{18} \cdot 100\% = \frac{9}{18} \cdot 100\% = 0,5 \cdot 100\% = 50\%;$

г) Среднее число неразгаданных слов: $\frac{1 \cdot 3 + 2 \cdot 6 + 3 \cdot 6 + 4 \cdot 3}{18} = \frac{3 + 12 + 18 + 12}{18} = \frac{45}{18} = 2,5;$

а) Таблица частот количества неразгаданных слов:

Общее количество всех учеников находится суммированием чисел по строке «Количество учеников». Вычисляем: $S = 3 + 6 + 6 + 3 = 18$. Это число показывает, что в исследовании участвовало 18 человек.

Чтобы найти частоты, делим количество учеников, соответствующих каждому числу неразгаданных слов, на общее количество учеников. Так:
для 1 неразгаданного слова $v_1 = \frac{3}{18}$. Так как $3$ учеников из $18$ имеют именно 1 неразгаданное слово, частота равна $\frac{3}{18}$. Выполним деление: $\frac{3}{18} = \frac{1}{6} \approx 0,17$.

для 2 неразгаданных слов $v_2 = \frac{6}{18}$. Так как $6$ учеников из $18$ имеют по 2 неразгаданных слова, получаем $\frac{6}{18} = \frac{1}{3} \approx 0,33$.

для 3 неразгаданных слов $v_3 = \frac{6}{18}$. Здесь также $6$ учеников, поэтому вычисления идентичны предыдущему случаю: $\frac{6}{18} = \frac{1}{3} \approx 0,33$.

для 4 неразгаданных слов $v_4 = \frac{3}{18}$. Число учеников снова равно 3, поэтому вычисляем: $\frac{3}{18} = \frac{1}{6} \approx 0,17$.

б) Построение полигона частот заключается в том, что по оси абсцисс откладываются значения признака (число неразгаданных слов: 1, 2, 3, 4), а по оси ординат — соответствующие им частоты (0,17; 0,33; 0,33; 0,17). Каждая точка соответствует паре (значение признака; частота), то есть (1;0,17), (2;0,33), (3;0,33), (4;0,17). Затем точки соединяются отрезками прямых. Полученный многоугольник и будет полигоном частот.

в) Для нахождения процента ребят, не разгадавших более двух слов, нужно сложить количество учеников, имеющих 3 и 4 неразгаданных слова. Это значения 6 и 3. Складываем: $6 + 3 = 9$. Таким образом, 9 человек из общего числа 18 имеют более двух неразгаданных слов. Теперь найдём долю: $\frac{9}{18} = 0,5$. Чтобы перевести эту долю в проценты, умножаем на 100: $0,5 \cdot 100\% = 50\%$. Это означает, что половина всех участников, то есть 50%, не разгадали более двух слов.

г) Чтобы найти среднее число неразгаданных слов, нужно вычислить среднее арифметическое, учитывая вес каждого значения признака. Для этого умножаем каждое значение признака на число учеников, которые ему соответствуют, складываем полученные произведения и делим результат на общее количество учеников.

Для 1 неразгаданного слова: $1 \cdot 3 = 3$.
Для 2 неразгаданных слов: $2 \cdot 6 = 12$.
Для 3 неразгаданных слов: $3 \cdot 6 = 18$.
Для 4 неразгаданных слов: $4 \cdot 3 = 12$.

Суммируем все произведения: $3 + 12 + 18 + 12 = 45$.

Теперь делим на общее количество учеников $18$: $\frac{45}{18} = 2,5$.

Таким образом, среднее число неразгаданных слов равно 2,5. Это значение означает, что в среднем каждый ученик не разгадал примерно 2,5 слова.