ГДЗ по Алгебре 9 Класс Остальные Задания Для Старого Учебника(2019) Номер 789 Дорофеев, Суворова — Подробные Ответы

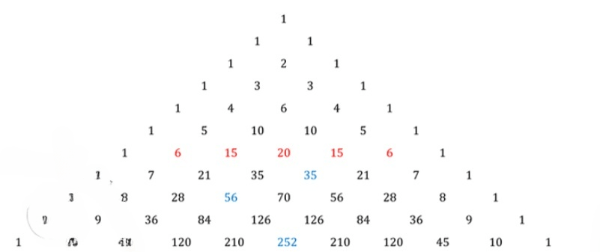
Вы, наверное, удивились, что число сочетаний из n по k обозначается так же, как и элемент треугольника Паскаля, расположенный в n-й строке на месте с номером k. Это не случайно, ведь это те же самые числа, они же — биномиальные коэффициенты.
1) Найдите по комбинаторной формуле, связывающей число сочетаний, размещений и перестановок, следующие сочетания: C(6; 1), C(6; 2), C(6; 3), C(6; 4), C(6; 5), C(6; 6). Сравните их с числами, стоящими в шестой строке треугольника Паскаля.
2) Найдите C(7; 4), C(8; 3), C(10; 5) по формуле и сравните с результатом, полученным с помощью треугольника Паскаля.

1) Найдем сочетания по формуле, связывающей перестановки, сочетания и размещения: $C_6^1 = \frac{A_6^1}{P_1} = \frac{6}{1} = 6;$ $C_6^2 = \frac{A_6^2}{P_2} = \frac{6 \cdot 5}{2!} = \frac{30}{2} = 15;$ $C_6^3 = \frac{A_6^3}{P_3} = \frac{6 \cdot 5 \cdot 4}{3!} = \frac{6 \cdot 5 \cdot 4}{3 \cdot 2} = 2 \cdot 5 \cdot 2 = 20;$ $C_6^4 = \frac{A_6^4}{P_4} = \frac{6 \cdot 5 \cdot 4 \cdot 3}{4!} = \frac{6 \cdot 5 \cdot 4 \cdot 3}{4 \cdot 3 \cdot 2} = 3 \cdot 5 = 15;$ $C_6^5 = \frac{A_6^5}{P_5} = \frac{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2}{5!} = \frac{6 \cdot 5!}{5!} = 6;$

2) Найдем сочетания по формуле: $C_7^4 = \frac{7!}{4! \cdot (7 — 4)!} = \frac{7 \cdot 6 \cdot 5 \cdot 4!}{4! \cdot 3!} = \frac{35 \cdot 6}{3 \cdot 2} = 35;$ $C_8^3 = \frac{8!}{3! \cdot (8 — 3)!} = \frac{8 \cdot 7 \cdot 6 \cdot 5!}{3 \cdot 2 \cdot 5!} = 8 \cdot 7 = 56;$ $C_{10}^5 = \frac{10!}{5! \cdot (10 — 5)!} = \frac{10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5!}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 5!} = 2 \cdot 3 \cdot 2 \cdot 7 \cdot 3 = 252;$

Все сочетания $C_n^k$ совпадают с элементами треугольника Паскаля, стоящими в $n$-ой строке и имеющими номер $k$:

1) Для нахождения сочетаний воспользуемся общей связью между перестановками, размещениями и сочетаниями. Формула имеет вид: $C_n^k = \frac{A_n^k}{P_k}$, где $A_n^k$ — число размещений из $n$ по $k$, а $P_k = k!$ — число перестановок из $k$ элементов. Таким образом, каждое сочетание есть отношение числа размещений к числу перестановок.

Для случая $C_6^1$:
Берём шесть элементов, выбираем один. Размещений $A_6^1 = 6$, так как можно выбрать любой из шести. Перестановок $P_1 = 1! = 1$. Тогда $C_6^1 = \frac{6}{1} = 6$. Это соответствует числу способов выбрать один элемент из шести.

Для случая $C_6^2$:
Размещений $A_6^2 = 6 \cdot 5 = 30$, так как первый элемент можно выбрать 6 способами, второй — 5 способами. Перестановок $P_2 = 2! = 2$. Тогда $C_6^2 = \frac{30}{2} = 15$. Это число способов выбрать два элемента из шести без учёта порядка.

Для случая $C_6^3$:
Размещений $A_6^3 = 6 \cdot 5 \cdot 4 = 120$. Перестановок $P_3 = 3! = 3 \cdot 2 \cdot 1 = 6$. Тогда $C_6^3 = \frac{120}{6} = 20$. Таким образом, существует 20 способов выбрать тройку элементов из шести.

Для случая $C_6^4$:
Размещений $A_6^4 = 6 \cdot 5 \cdot 4 \cdot 3 = 360$. Перестановок $P_4 = 4! = 24$. Тогда $C_6^4 = \frac{360}{24} = 15$. Здесь результат совпадает с $C_6^2$, так как выбор четырёх элементов из шести эквивалентен выбору двух элементов, которые исключаются.

Для случая $C_6^5$:
Размещений $A_6^5 = 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 = 720$. Перестановок $P_5 = 5! = 120$. Тогда $C_6^5 = \frac{720}{120} = 6$. Очевидно, что выбор пяти элементов из шести равнозначен выбору одного элемента, который исключается, поэтому результат совпадает с $C_6^1$.

2) Теперь используем стандартную формулу сочетаний $C_n^k = \frac{n!}{k!(n-k)!}$, где $n!$ — факториал числа $n$.

Для случая $C_7^4$:
$7! = 7 \cdot 6 \cdot 5 \cdot 4!$. Подставляем в формулу: $C_7^4 = \frac{7!}{4!(7-4)!} = \frac{7 \cdot 6 \cdot 5 \cdot 4!}{4! \cdot 3!}$. Сокращаем одинаковые множители $4!$: остаётся $\frac{7 \cdot 6 \cdot 5}{3 \cdot 2 \cdot 1}$. Числитель равен $210$, знаменатель равен $6$. Делим: $210 : 6 = 35$. Следовательно, $C_7^4 = 35$.

Для случая $C_8^3$:
$8! = 8 \cdot 7 \cdot 6 \cdot 5!$. Подставляем: $C_8^3 = \frac{8!}{3!(8-3)!} = \frac{8 \cdot 7 \cdot 6 \cdot 5!}{3! \cdot 5!}$. Сокращаем $5!$. Остаётся $\frac{8 \cdot 7 \cdot 6}{3 \cdot 2 \cdot 1}$. Числитель равен $336$, знаменатель равен $6$. Делим: $336 : 6 = 56$. Таким образом, $C_8^3 = 56$.

Для случая $C_{10}^5$:
$10! = 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5!$. Подставляем: $C_{10}^5 = \frac{10!}{5!(10-5)!} = \frac{10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5!}{5! \cdot 5!}$. Сокращаем один $5!$. Остаётся $\frac{10 \cdot 9 \cdot 8 \cdot 7 \cdot 6}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}$. Вычисляем числитель: $10 \cdot 9 = 90$, $90 \cdot 8 = 720$, $720 \cdot 7 = 5040$, $5040 \cdot 6 = 30240$. Знаменатель равен $120$. Делим: $30240 : 120 = 252$. Таким образом, $C_{10}^5 = 252$.

Все полученные результаты соответствуют значениям в треугольнике Паскаля. Каждый элемент $C_n^k$ в треугольнике Паскаля располагается в $n$-й строке и соответствует номеру $k$. Например, для $n = 6$ строка содержит значения $1, 6, 15, 20, 15, 6, 1$, которые полностью совпадают с вычисленными $C_6^k$ для $k = 1, 2, 3, 4, 5$.