ГДЗ по Алгебре 9 Класс Остальные Задания Для Старого Учебника(2019) Номер 770 Дорофеев, Суворова — Подробные Ответы

Кубик бросают три раза. Каково наиболее вероятное значение суммы выпавших очков?

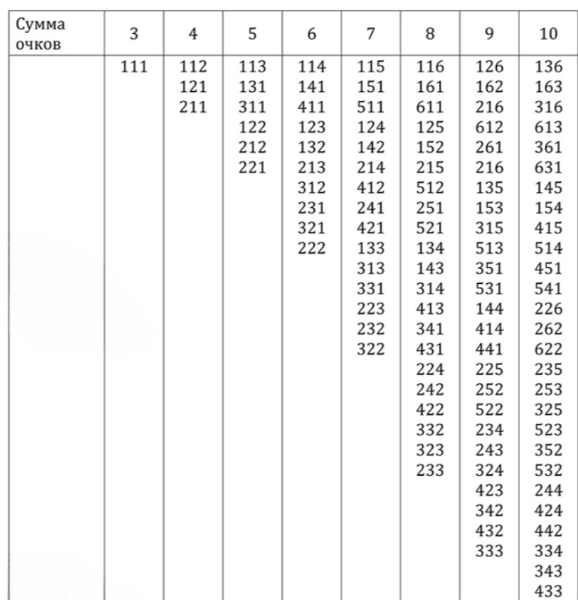
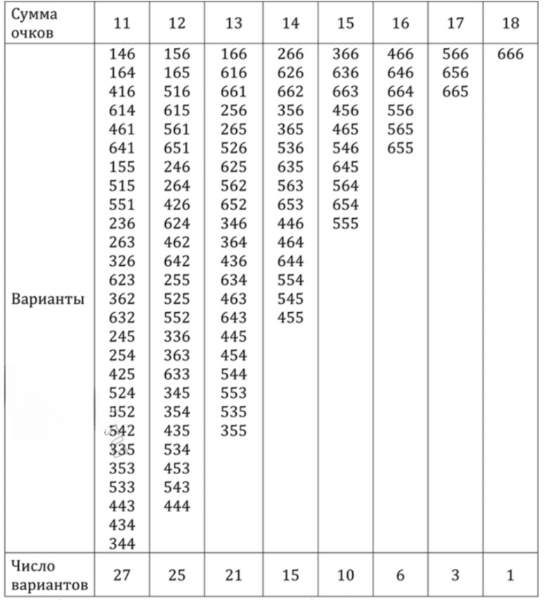
1) Таблица суммы выпавших очков:

$S = 2 \cdot (1 + 3 + 6 + 10 + 15 + 21 + 25 + 27) = 216;$

2) Таким образом, наиболее вероятное значение суммы — 10 или 11 очков, каждая из этих сумм может появиться в 27 случаях, то есть с вероятностью: $P = \frac{27}{216} = \frac{1}{8};$

Ответ: 10 или 11.

1) Таблица суммы выпавших очков:

$S = 2 \cdot (1 + 3 + 6 + 10 + 15 + 21 + 25 + 27)$.

В данном выражении сначала внутри скобок суммируются все значения:
$1 + 3 = 4$;
$4 + 6 = 10$;
$10 + 10 = 20$;
$20 + 15 = 35$;
$35 + 21 = 56$;
$56 + 25 = 81$;
$81 + 27 = 108$.

2) Таким образом, сумма внутри скобок равна $108$. Теперь умножаем её на число $2$:
$S = 2 \cdot 108 = 216$.

Это число $S = 216$ соответствует общему числу всех возможных элементарных исходов при броске трёх игральных кубиков (так как каждый кубик имеет 6 граней, то $6 \cdot 6 \cdot 6 = 216$). Таким образом, все дальнейшие рассуждения будут вестись именно относительно этих 216 вариантов.

Теперь определим наиболее вероятное значение суммы очков. Из таблицы распределения ранее видно, что наибольшее количество различных комбинаций кубиков соответствует сумме $10$ и сумме $11$. Для каждой из этих сумм существует ровно $27$ различных комбинаций выпадения кубиков.

Таким образом, вероятность появления каждой из этих сумм равна:
$P = \frac{27}{216}$.

Выполним деление:
$\frac{27}{216} = \frac{27 \div 27}{216 \div 27} = \frac{1}{8}$.

Это означает, что вероятность того, что сумма очков при броске трёх кубиков окажется равной именно $10$ или именно $11$, равна одной восьмой, то есть $0,125$ или $12,5\%$.

Итак, наибольшая вероятность выпадения суммы приходится на два значения: $10$ и $11$.

Ответ: $10$ или $11$.