ГДЗ по Алгебре 9 Класс Остальные Задания Для Старого Учебника(2019) Номер 749 Дорофеев, Суворова — Подробные Ответы

В небоскрёбе 90 этажей. За день лифт вызывали на каждый этаж несколько раз; на первый этаж лифт вызывали 29 раз, на второй — 9 раз, на третий — 27 раз и т. д. К вечеру получилось, что число вызовов составляет следующий ряд (в порядке возрастания номера этажа):
29, 9, 27, 11, 18, 6, 20, 21, 7, 12, 25, 28, 22, 21, 19, 23, 15,
24, 13, 19, 17, 26, 17, 24, 8, 10, 13, 16, 27, 15, 14, 27, 11,
20, 9, 15, 6, 17, 22, 23, 12, 19, 7, 16, 24, 12, 5, 14, 26, 5, 10,
21, 17, 8, 25, 18, 29, 21, 17, 15, 28, 12, 26, 22, 10, 26, 11,
18, 16, 22, 29, 13, 6, 20, 7, 19, 23, 28, 13, 5, 20, 14, 7, 15,
16, 19, 8, 22, 18, 14.
а) Постройте для данного ряда интервальный ряд (определите размах ряда, возьмите длину промежутка, равную 4 единицам, и вычислите границы интервалов).
б) Для интервального ряда составьте таблицу частот.
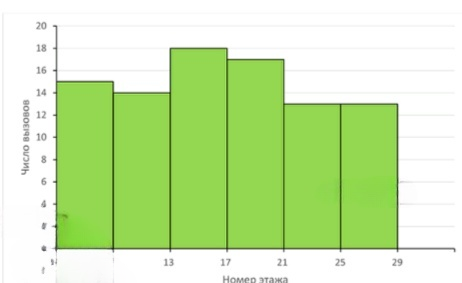
в) Постройте гистограмму частот.

а) Размах ряда:
$29 — 5 = 24$;

Пусть длина интервала равна $4$, тогда границы интервалов:
$5 — 9$; $9 — 13$; $13 — 17$; $17 — 21$; $21 — 25$; $25 — 29$;

б) Таблица частот для интервального ряда:

$S = 15 + 14 + 18 + 17 + 13 + 13 = 90$;

$v_{5-9} = \frac{15}{90} \approx 0,17$;
$v_{9-13} = \frac{14}{90} \approx 0,16$;
$v_{13-17} = \frac{18}{90} = 0,2$;
$v_{17-21} = \frac{17}{90} \approx 0,19$;
$v_{21-25} = \frac{13}{90} \approx 0,14$;
$v_{25-29} = \frac{13}{90} \approx 0,14$;

в) Гистограмма частот:

а) Размах ряда определяется как разность между наибольшим и наименьшим значением выборки. Так как наибольшее значение равно $29$, а наименьшее равно $5$, то получаем:
$R = 29 — 5 = 24$.

Чтобы построить интервальный ряд, необходимо разделить диапазон значений на равные интервалы. Пусть длина интервала равна $h = 4$. Тогда последовательные интервалы будут иметь границы:
$5 — 9$, $9 — 13$, $13 — 17$, $17 — 21$, $21 — 25$, $25 — 29$.

б) Далее строим таблицу частот. Для каждого интервала подсчитываем количество наблюдений (число вызовов) и определяем относительные частоты (доли от общего числа наблюдений).

Сначала подсчитаем общее количество наблюдений:
$S = 15 + 14 + 18 + 17 + 13 + 13 = 90$.

Теперь вычислим частоты для каждого интервала как отношение числа наблюдений в интервале к общему числу наблюдений:

Для интервала $5 — 9$:
$v_{5-9} = \frac{15}{90} = \frac{1}{6} \approx 0,17$.

Для интервала $9 — 13$:
$v_{9-13} = \frac{14}{90} \approx 0,16$.

Для интервала $13 — 17$:
$v_{13-17} = \frac{18}{90} = 0,2$.

Для интервала $17 — 21$:
$v_{17-21} = \frac{17}{90} \approx 0,19$.

Для интервала $21 — 25$:
$v_{21-25} = \frac{13}{90} \approx 0,14$.

Для интервала $25 — 29$:
$v_{25-29} = \frac{13}{90} \approx 0,14$.

Таким образом, полученные частоты показывают относительное распределение вызовов по каждому температурному интервалу.

в) Гистограмма частот.
На оси абсцисс откладываются интервалы $5 — 9$, $9 — 13$, $13 — 17$, $17 — 21$, $21 — 25$, $25 — 29$.
На оси ординат откладываются частоты.
Высоты прямоугольников соответствуют значениям $0,17$, $0,16$, $0,2$, $0,19$, $0,14$, $0,14$.

Каждый прямоугольник строится на соответствующем интервале и имеет площадь, пропорциональную частоте. Гистограмма наглядно показывает, что максимальная частота достигается в интервале $13 — 17$, где сосредоточено $20\%$ всех наблюдений.

Ответ: размах равен $24$, частоты рассчитаны и приведены в таблице, а гистограмма отражает распределение данных по интервалам.