ГДЗ по Алгебре 9 Класс Остальные Задания Для Старого Учебника(2019) Номер 721 Дорофеев, Суворова — Подробные Ответы

В 2008 г. население каждого из угледобывающих посёлков А и В составляло примерно 30 тыс. человек. В связи с истощением месторождений люди начали переезжать в другие места. В каждый год из следующих четырёх лет численность населения посёлка А можно было определить по формуле $A_n = 30000 — 2500n$, а посёлка В — по формуле $B_n = 30000 \cdot 0,7^n$, где $n$ — число лет, прошедших после 2008 г.
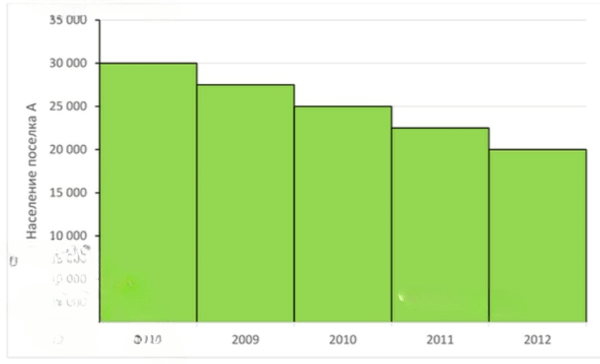
В каком из посёлков численность населения изменялась в арифметической прогрессии, а в каком — в геометрической? Продолжите построение диаграммы для каждого случая (Рис. 4.20).

1) Население поселка $A$ через $n$ лет:
$A_n = 30\,000 — 2500n$;

Изменяется в арифметической прогрессии:
$A_1 = 30\,000 — 2500 \cdot 1 = 30\,000 — 2\,500 = 27\,500$;
$A_2 = 30\,000 — 2500 \cdot 2 = 30\,000 — 5\,000 = 25\,000$;
$A_3 = 30\,000 — 2500 \cdot 3 = 30\,000 — 7\,500 = 22\,500$;
$A_4 = 30\,000 — 2500 \cdot 4 = 30\,000 — 10\,000 = 20\,000$;

Диаграмма:

1) Население поселка $B$ через $n$ лет:
$B_n = 30\,000 \cdot 0,7^n$;

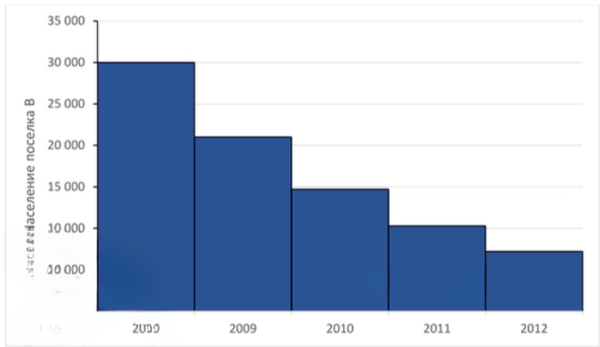
Изменяется в геометрической прогрессии:
$B_1 = 30\,000 \cdot 0,7^1 = 21\,000$;
$B_2 = 30\,000 \cdot 0,7^2 = 30\,000 \cdot 0,49 = 14\,700$;
$B_3 = 30\,000 \cdot 0,7^3 = 30\,000 \cdot 0,343 = 10\,290$;
$B_4 = 30\,000 \cdot 0,7^4 = 30\,000 \cdot 0,2401 = 7\,203$;

Диаграмма:

1) Для посёлка $A$ формула: $A_n = 30\,000 — 2500n$.
Эта запись означает, что начальное население в 2008 году равно $30\,000$, а каждый год численность уменьшается на одинаковое количество жителей — на $2500$ человек. Такая закономерность является признаком арифметической прогрессии, так как разность между соседними членами постоянна и равна $d = -2500$.

Вычислим первые члены:
Для $n = 1$: $A_1 = 30\,000 — 2500 \cdot 1 = 27\,500$.
Для $n = 2$: $A_2 = 30\,000 — 2500 \cdot 2 = 25\,000$.
Для $n = 3$: $A_3 = 30\,000 — 2500 \cdot 3 = 22\,500$.
Для $n = 4$: $A_4 = 30\,000 — 2500 \cdot 4 = 20\,000$.

Можно заметить, что разность $A_{n+1} — A_n = -2500$ сохраняется. Это подтверждает, что последовательность населения посёлка $A$ является арифметической прогрессией. Все значения уменьшаются равномерно с шагом $2500$.

Диаграмма будет линейно убывающей, так как члены образуют арифметическую прогрессию.

1) Для посёлка $B$ формула: $B_n = 30\,000 \cdot 0,7^n$.
Эта запись означает, что начальное население в 2008 году равно $30\,000$, а каждый следующий год оно уменьшается не на одно и то же число, а в одинаковое количество раз — умножением на коэффициент $0,7$. Это соответствует геометрической прогрессии с первым членом $b_1 = 30\,000 \cdot 0,7$ и знаменателем $q = 0,7$.

Вычислим первые члены:
Для $n = 1$: $B_1 = 30\,000 \cdot 0,7^1 = 21\,000$.
Для $n = 2$: $B_2 = 30\,000 \cdot 0,7^2 = 30\,000 \cdot 0,49 = 14\,700$.
Для $n = 3$: $B_3 = 30\,000 \cdot 0,7^3 = 30\,000 \cdot 0,343 = 10\,290$.
Для $n = 4$: $B_4 = 30\,000 \cdot 0,7^4 = 30\,000 \cdot 0,2401 = 7\,203$.

Видно, что отношение $\frac{B_{n+1}}{B_n} = 0,7$ постоянно. Это подтверждает, что последовательность является геометрической прогрессией. Население уменьшается в 0,7 раза каждый год.

Диаграмма для посёлка $B$ будет экспоненциально убывающей: значения уменьшаются быстро в первые годы, а затем медленнее, приближаясь к нулю, но никогда его не достигая.

Ответ:
— в посёлке $A$ население изменяется по арифметической прогрессии с разностью $-2500$;
— в посёлке $B$ население изменяется по геометрической прогрессии со знаменателем $0,7$.