ГДЗ по Алгебре 9 Класс Остальные Задания Для Старого Учебника(2019) Номер 6 Дорофеев, Суворова — Подробные Ответы

Множество натуральных чисел N включается в множество целых чисел Z.
На языке символов это записывается так: $N \subset Z$ — и читается: «Всякое натуральное число является целым».
Схематически соотношение между множествами $N$ и $Z$ показано на рисунке 1.2.
Прочитайте и изобразите с помощью схемы соотношение:
$Z \subset Q$, $Q \subset R$, $Z \subset R$, $N \subset Z \subset Q$, $N \subset Z \subset Q \subset R$.

$\mathbb{Z} \subset \mathbb{Q}$:

Всякое целое число является рациональным;

$\mathbb{Q} \subset \mathbb{R}$:

Всякое рациональное число является действительным;

$\mathbb{Z} \subset \mathbb{R}$:

Всякое целое число является действительным;

$\mathbb{N} \subset \mathbb{Z} \subset \mathbb{R}$:

Всякое натуральное число является целым, а всякое целое число является действительным;

$\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}$:

Всякое натуральное число является целым, всякое целое число является рациональным, а всякое рациональное число — действительным;

Множество натуральных чисел $N$ включается в множество целых чисел $Z$. Это означает, что каждый элемент множества $N$ обязательно содержится в множестве $Z$. На языке символов данное включение записывается как $N \subset Z$. Такая запись читается следующим образом: «Всякое натуральное число является целым числом».

Схематически это можно изобразить в виде кругов: меньший круг $N$ находится внутри большего круга $Z$. Это отражает, что любое число из $N$ входит и в $Z$.

Теперь аналогично рассмотрим все остальные включения:

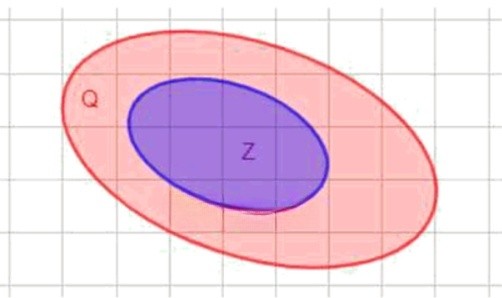
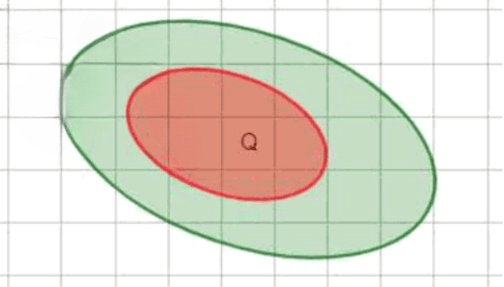
$Z \subset Q$. Это утверждение обозначает, что множество целых чисел $Z$ включено в множество рациональных чисел $Q$. Иными словами, любое целое число можно представить в виде дроби $\frac{m}{n}$, где знаменатель $n = 1$. Например, число $-7$ можно записать как $\frac{-7}{1}$. Таким образом, каждое целое число является рациональным.

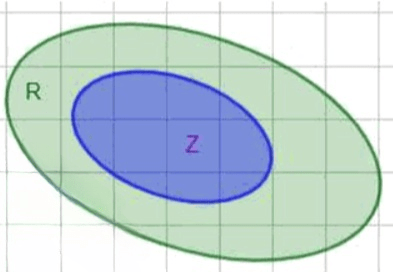
$Q \subset R$. Это означает, что множество рациональных чисел $Q$ включено во множество действительных чисел $R$. Рациональные числа — это частный случай действительных, так как действительные включают и рациональные, и иррациональные. Например, $\frac{2}{5} \in Q$ и одновременно $\frac{2}{5} \in R$.

$Z \subset R$. Это означает, что множество целых чисел $Z$ включено во множество действительных чисел $R$. Каждое целое число — это действительное число, так как оно имеет точное место на числовой прямой. Например, $10 \in Z$ и одновременно $10 \in R$.

$N \subset Z \subset Q$. Здесь указывается последовательность вложений. Натуральные числа $N$ являются частью множества целых $Z$, а целые $Z$, в свою очередь, входят в рациональные $Q$. Например, число $5 \in N$, значит, $5 \in Z$, и так как $5 = \frac{5}{1}$, то $5 \in Q$.

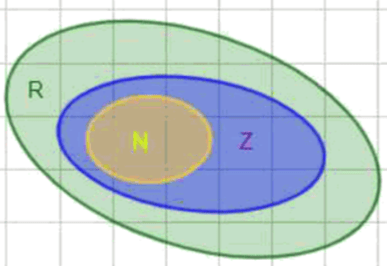
$N \subset Z \subset Q \subset R$. Это расширенная цепочка включений, показывающая полное вложение множеств. Натуральные числа $N$ входят в целые $Z$, целые входят в рациональные $Q$, а рациональные входят в действительные $R$. Таким образом, любое натуральное число также является и целым, и рациональным, и действительным. Например, число $12 \in N$, значит, $12 \in Z$, $12 = \frac{12}{1} \in Q$, и, наконец, $12 \in R$.

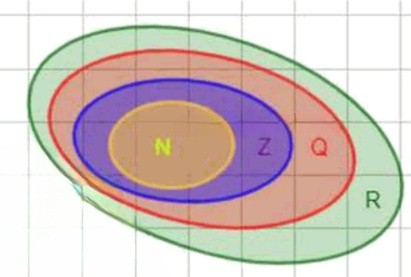
Все эти включения можно изобразить схемой вложенных множеств:
$N \subset Z \subset Q \subset R$.