ГДЗ по Алгебре 9 Класс Остальные Задания Для Старого Учебника(2019) Номер 558 Дорофеев, Суворова — Подробные Ответы

1) Докажите алгебраическим методом, что система уравнений

$\{\begin{array}{l}2x-y=4\\ x+y=2\\ x^2+y^2=4\end{array}$

имеет решение, и притом только одно. Дайте графическую иллюстрацию данного утверждения.

2) Найдите такое значение $r$, при котором система уравнений

$\{\begin{array}{l}x-y=-3\\ x+2y=6\\ x^2+y^2=r^2\end{array}$

имеет решение.

I)

Доказательство алгебраическим методом:

$\{\begin{array}{l}2x-y=4\\ x+y=2\\ x^2+y^2=4\end{array}$

Решим систему из первых двух уравнений:

$\mathrm{1)\; 2}x-y=4,$ отсюда $y=2x-4;$

$\mathrm{2)\; x}+2x-4=2;$

$3x=2+4;$

$3x=6,$ отсюда $x=2;$

$y=2\cdot 2-4=4-4=0;$

Проверим, является ли оно решением третьего уравнения:

$2^2+0^2=4;$

$4=4\text{— верно;}$

Графическая иллюстрация:

$\mathrm{1)\; 2}x-y=4=>y=2x-4\text{— уравнение прямой:}$

$\mathrm{2)\; x}+y=2=>y=2-x\text{— уравнение прямой:}$

${\mathrm{3)\; x}}^2+y^2=4\text{— уравнение окружности:}$

$x_0=0$ и $y_0=0,$ $R=\sqrt{4}=2;$

функций пересекаются только в одной точке;

II)

$\{\begin{array}{l}x-y=-3\\ x+2y=6\\ x^2+y^2=r^2\end{array}$

$\mathrm{1)\; x}-y=-3,$ отсюда $y=x+3;$

$\mathrm{2)\; x}+2(x+3)=6;$

$x+2x+6=6;$

$3x=6-6;$

$3x=0,$ отсюда $x=0;$

$y=0+3=3;$

${\mathrm{3)\; r}}^2=0^2+3^2;$

$r^2=9,$ отсюда $r=\pm 3;$

Ответ: $r=\pm 3.$

I)

Доказательство алгебраическим методом:

$\{\begin{array}{l}2x-y=4\\ x+y=2\\ x^2+y^2=4\end{array}$

Из первого уравнения $2x-y=4$ выразим $y$ через $x$:

$$y=2x-4.$$

Подставим $y=2x-4$ во второе уравнение $x+y=2$:

$$x+(2x-4)=2.$$

Упростим:

$$3x-4=2.$$

Теперь перенесем -4 в правую часть:

$$3x=2+4\Rightarrow 3x=6\Rightarrow x=\frac{6}{3}=2.$$

Подставим $x=2$ в $y=2x-4$:

$$y=2\cdot 2-4=4-4=0.$$

Проверим, является ли найденное решение $x=2$ и $y=0$ решением третьего уравнения $x^2+y^2=4$:

$$2^2+0^2=4\Rightarrow 4=4\text{— верно.}$$

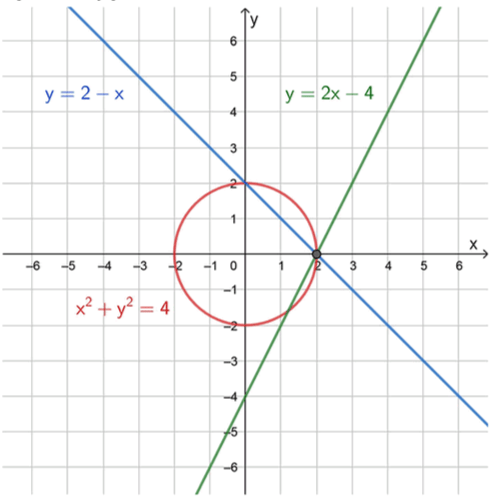
Графическая иллюстрация:

Уравнение $2x-y=4$ преобразуется в $y=2x-4$, это уравнение прямой. Подставим разные значения $x$ для построения таблицы:

$$\overline{)\begin{array}{cc}x& y\\ 0& -4\\ 2& 0\end{array}}$$

Уравнение $x+y=2$ преобразуется в $y=2-x$, это также уравнение прямой. Подставим разные значения $x$:

$$\overline{)\begin{array}{cc}x& y\\ 0& 2\\ 2& 0\end{array}}$$

Уравнение $x^2+y^2=4$ — это уравнение окружности с центром в $(0,0)$ и радиусом $R=\sqrt{4}=2$. Подставим значения $x$ и найдем $y$:

$$\overline{)\begin{array}{cc}x& y\\ 2& 0\\ 0& 2\end{array}}$$

Все три графика пересекаются только в одной точке $(2,0)$.

Ответ: $(2;0)$.

II)

$\{\begin{array}{l}x-y=-3\\ x+2y=6\\ x^2+y^2=r^2\end{array}$

Из первого уравнения $x-y=-3$ выразим $y$ через $x$:

$$y=x+3.$$

Подставим $y=x+3$ во второе уравнение $x+2y=6$:

$$x+2(x+3)=6.$$

Раскроем скобки:

$$x+2x+6=6\Rightarrow 3x+6=6.$$

Теперь перенесем 6 в правую часть:

$$3x=6-6\Rightarrow 3x=0\Rightarrow x=0.$$

Подставим $x=0$ в $y=x+3$:

$$y=0+3=3.$$

Подставим $x=0$ и $y=3$ в уравнение $x^2+y^2=r^2$:

$$0^2+3^2=r^2\Rightarrow 9=r^2\Rightarrow r=\pm 3.$$

Ответ: $r=\pm 3$.