ГДЗ по Алгебре 9 Класс Остальные Задания Для Старого Учебника(2019) Номер 337 Дорофеев, Суворова — Подробные Ответы

а) Докажите, что выражение $\frac{-15}{2x^2-3x+3}$ при любых значениях $x$ принимает отрицательные значения.

б) Докажите, что выражение $\frac{-24}{-3x^2+10x-9}$ ни при каких значениях $x$ не принимает отрицательные значения.

а) $\frac{-15}{2x^2-3x+3}<0$;

$1)\; -15<0$, то есть требуется найти значения $x$ при которых:
$2x^2-3x+3>0$;

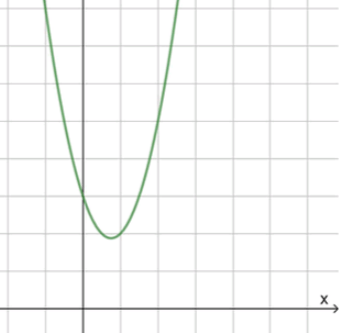
$\mathrm{2)\; a}=2>0$, значит ветви параболы направлены вверх;

3) Нули функции:
$2x^2-3x+3=0$;
$D=3^2-4\cdot 2\cdot 3=9-24=-15$;
$D⩽0$, значит корней нет;

4) Схематичный рисунок:

$x\in (-\mathrm{\infty };+\mathrm{\infty })$, что и требовалось доказать.

б) $\frac{-24}{-3x^2+10x-9}<0$;

$1)\; -24<0$, то есть требуется найти значения $x$ при которых:
$-3x^2+10x-9>0$;

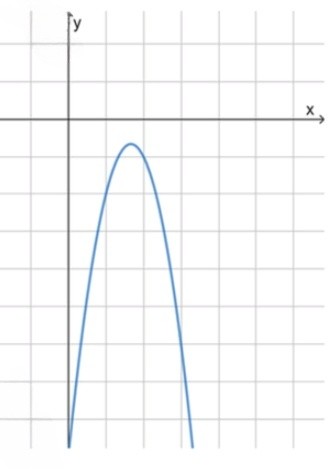
$\mathrm{2)\; a}=-3<0$, значит ветви параболы направлены вниз;

3) Нули функции:
$-3x^2+10x-9=0$;
$D={10}^2-4\cdot 3\cdot 9=100-108=-8$;
$D<0$, значит корней нет;

4) Схематичный рисунок:

$x\in \mathrm{\varnothing }$, что и требовалось доказать.

а) $\frac{-15}{2x^2-3x+3}<0$;

Числитель равен числу $-15$, которое меньше нуля: $-15<0$. Значит, чтобы вся дробь была отрицательной, знаменатель должен быть положительным, так как при делении отрицательного числа на положительное результат будет меньше нуля: $\frac{-}{+}=-$. Таким образом, нужно найти те значения переменной $x$, при которых выражение в знаменателе $2x^2-3x+3$ больше нуля:

$2x^2-3x+3>0$

Это квадратный трёхчлен. Коэффициент при $x^2$ равен $a=2$, и он положителен ($2>0$), значит, графиком будет парабола с ветвями, направленными вверх. Чтобы выяснить, где этот трёхчлен больше нуля, найдем его корни:

$2x^2-3x+3=0$

Находим дискриминант:

$D=(-3{)}^2-4\cdot 2\cdot 3=9-24=-15$

Так как дискриминант меньше нуля ($D<0$), у уравнения нет действительных корней. Это означает, что парабола не пересекает ось $x$, а так как ветви направлены вверх, то вся парабола находится выше оси $x$, и значит выражение $2x^2-3x+3$ всегда положительно при любом значении $x$. Следовательно, неравенство выполняется для всех действительных $x$.

Ответ: $x\in (-\mathrm{\infty };+\mathrm{\infty })$

б) $\frac{-24}{-3x^2+10x-9}<0$;

Числитель равен числу $-24$, которое меньше нуля: $-24<0$. Чтобы вся дробь была отрицательной, необходимо, чтобы знаменатель был положительным: $\frac{-}{+}=-$. Ищем такие значения переменной $x$, при которых выражение в знаменателе $-3x^2+10x-9$ положительно:

$-3x^2+10x-9>0$

Это снова квадратный трёхчлен. Коэффициент при $x^2$ равен $a=-3$, и он отрицателен ($-3<0$), значит, график — парабола с ветвями, направленными вниз. Попробуем найти корни уравнения:

$-3x^2+10x-9=0$

Находим дискриминант:

$D={10}^2-4\cdot (-3)\cdot (-9)=100-108=-8$

Так как дискриминант отрицательный ($D<0$), уравнение не имеет действительных корней. Это значит, что парабола не пересекает ось $x$, и вся парабола лежит либо выше оси $x$, либо ниже. Так как ветви направлены вниз, и нет точек пересечения с осью, вершина параболы лежит выше оси, а вся остальная часть ниже оси. Следовательно, значение выражения $-3x^2+10x-9$ всегда меньше нуля при любом $x$, то есть:

$-3x^2+10x-9<0\text{для всех }x\in \mathbb{R}$

А нам нужно, чтобы выражение в знаменателе было положительным. Но оно нигде не положительно, а значит, нет таких значений $x$, при которых вся дробь была бы меньше нуля.

Ответ: $x\in \mathrm{\varnothing }$