
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Остальные Задания Для Старого Учебника(2019) Номер 335 Дорофеев, Суворова — Подробные Ответы
Найдите целые решения неравенства:
а) ;
б) ;
в) ;
г) .
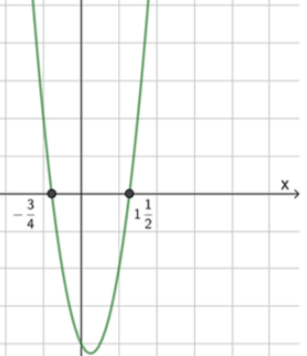
а) :
Умножим обе части на 12:
, значит ветви направлены вверх;
2) Нули функции:
3) Схематический рисунок
Целые решения:
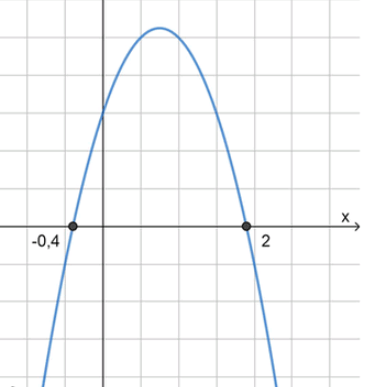
б) :
Умножим обе части на 6:
, значит ветви направлены вниз;
2) Нули функции:
3) Схематический рисунок
-0,4 < х < 2;
Целые решения:
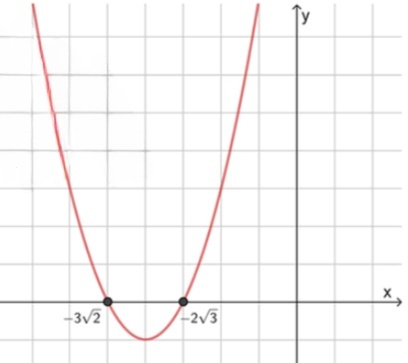
в) :
, значит ветви направлены вверх;
2) Нули функции:
3) Схематический рисунок
Целое решение:
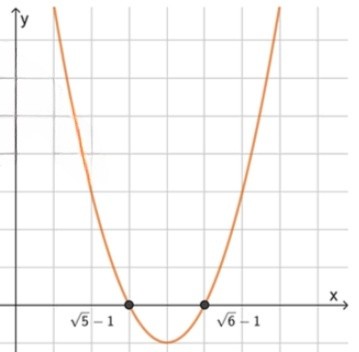
г) :
, значит ветви направлены вверх;
2) Нули функции:
3) Схематический рисунок
Целые решения отсутствуют.
а)
умножим обе части неравенства на 12 (наименьшее общее кратное знаменателей 3 и 4), чтобы избавиться от дробей:
переносим все слагаемые в левую часть и приводим подобные:
это квадратное неравенство с коэффициентами:
так как , ветви параболы направлены вверх, значит выражение меньше нуля между корнями
находим дискриминант:
так как , уравнение имеет два различных вещественных корня
находим корни по формуле:
так как неравенство строгое и парабола вверх, решением будет промежуток между корнями:
целые числа, принадлежащие этому промежутку: 0 и 1
ответ:
б)
умножаем обе части на 6:
переносим все влево:
или
умножим на (-1), при этом меняется знак неравенства
коэффициенты:
ветви параболы направлены вниз, так как
находим дискриминант:
корни:
решение неравенства:
целые числа из этого промежутка: 0 и 1
ответ:
в)
здесь произведение двух линейных множителей, значит корни:
поскольку
так как коэффициент при
приблизительно:
единственное целое число в этом промежутке —
ответ:
г)
корни:
меньший корень:
ветви параболы направлены вверх, значит неравенство выполняется на отрезке между корнями включительно:
в этом отрезке нет целых чисел
ответ: нет решений




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!