ГДЗ по Алгебре 9 Класс Остальные Задания Для Старого Учебника(2019) Номер 332 Дорофеев, Суворова — Подробные Ответы

Постройте график функции и определите, при каких значениях a прямая y=a имеет с графиком три общие точки; две общие точки; одну общую точку:

$\mathrm{а)\; y}=\{\begin{array}{ll}4-x^2,& \text{если }x\le 2;\\ x-2,& \text{если }x>2;\end{array}$

$\mathrm{б)\; y}=\{\begin{array}{ll}x,& \text{если }x\le -1;\\ x^2-2,& \text{если }x>-1;\end{array}$

а) $y=\{\begin{array}{ll}4-x^2,& \text{если }x\le 2;\\ x-2,& \text{если }x>2;\end{array}$

$\mathrm{1)\; y}=4-x^2$ — уравнение параболы:

$x_0=0$ и $y_0=4$;

$\overline{)\begin{array}{cccccc}x& -3& -2& -1& 1& 2\\ y& -5& 0& 3& 3& 0\end{array}}$

$\mathrm{2)\; y}=x-2$ — уравнение прямой:

$\overline{)\begin{array}{ccc}x& 2& 4\\ y& 0& 2\end{array}}$

График искомой функции:

3) График имеет с прямой $y=a$:

Одну общую точку при $x\in (-\mathrm{\infty };0)\cup (4;+\mathrm{\infty })$;

Две общие точки при $x=0$ и $x=4$;

Три общие точки при $x\in (0;4)$;

б) $y=\{\begin{array}{ll}x,& \text{если }x\le -1;\\ x^2-2,& \text{если }x>-1;\end{array}$

$\mathrm{1)\; y}=x$ — уравнение прямой:

$\overline{)\begin{array}{ccc}x& -2& -1\\ y& -2& -1\end{array}}$

$\mathrm{2)\; y}=x^2-2$ — уравнение параболы:

$x_0=0$ и $y_0=-2$;

$\overline{)\begin{array}{ccccc}x& -1& 1& 2& 3\\ y& -1& -1& 2& 7\end{array}}$

График искомой функции:

3) График имеет с прямой $y=a$:

Одну общую точку при $x\in (-\mathrm{\infty };-2)\cup (-1;+\mathrm{\infty })$;

Две общие точки при $x=-2$ и $x=-1$;

Три общие точки при $x\in (-2;-1)$;

а) $y=\{\begin{array}{ll}4-x^2,& \text{если }x\le 2;\\ x-2,& \text{если }x>2;\end{array}$

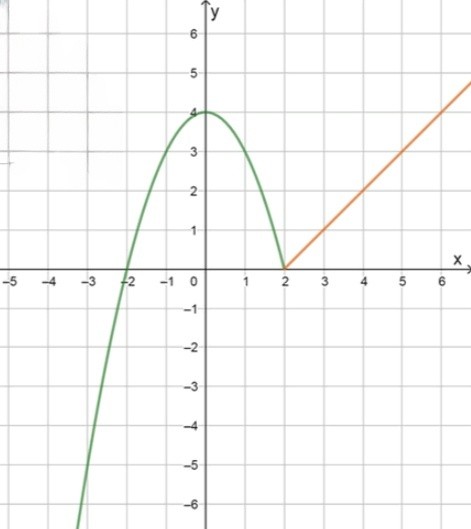
Первая часть функции — это ветвь параболы с ветвями вниз, так как перед $x^2$ стоит минус. Вершина параболы находится в точке $x_0=0$, так как функция имеет вид $y=-x^2+4$. Подставим $x=0$:
$y=4-0^2=4$, значит вершина — точка $(0;4)$.

Заполним таблицу значений на интервале $x\le 2$:
При $x=-3$: $y=4-(-3{)}^2=4-9=-5$
При $x=-2$: $y=4-4=0$
При $x=-1$: $y=4-1=3$
При $x=1$: $y=4-1=3$
При $x=2$: $y=4-4=0$

$\overline{)\begin{array}{cccccc}x& -3& -2& -1& 1& 2\\ y& -5& 0& 3& 3& 0\end{array}}$

Вторая часть функции — это линейная функция $y=x-2$, определённая на области $x>2$. Построим таблицу значений:

При $x=2$: $y=2-2=0$
При $x=4$: $y=4-2=2$

$\overline{)\begin{array}{ccc}x& 2& 4\\ y& 0& 2\end{array}}$

График состоит из двух частей: ветви параболы (слева от и включая точку $x=2$) и луча прямой (справа от точки $x=2$, но сама точка $x=2$ не включается во вторую часть). При $x=2$ обе части дают одно и то же значение: $y=0$, значит график непрерывен в точке склейки.

Определим, при каких значениях $a$ прямая $y=a$ имеет с графиком:

– одну общую точку:
Пусть $y=a$ проходит так, что она пересекает график один раз. Это возможно, если она касается только параболы (одна точка) или только прямой (одна точка). Для касания параболы возможна точка максимума — вершина. Вершина параболы: $y=4$, точка касания — одна.
Также возможны случаи, когда горизонтальная прямая находится ниже минимального значения функции: парабола и прямая $x-2$ не будут пересекаться одновременно.
Итак, одна точка — при $y>4$, когда она пересекает только прямую, или $y<-5$, когда она пересекает только параболу. Ещё один случай — $y=4$, касание в вершине.
Ответ: $a\in (-\mathrm{\infty };-5)\cup (4;+\mathrm{\infty })\cup \{4\}$

– две общие точки:
Прямая пересекает график в двух точках, когда одна из точек на параболе, другая — на прямой. Это возможно, когда прямая находится между минимальным и максимальным значением графика.
Парабола достигает максимум 4, минимум — $-5$. Прямая от $x=2$ идёт вверх. Таким образом, если $a=0$, прямая пересекает параболу в двух точках, а прямую — в одной, итого 3. Если $a=-5$ или $a=2$, возможны касания.
Чтобы было ровно 2 точки, нужно, чтобы прямая прошла через одну часть графика и касалась другой — либо касание вершины параболы $y=4$, либо касание прямой в точке $x=2$. Значения: $a=0$, если обе точки на одной части, или касание и одна точка на другой.
Точные значения: $a=-5$ (график касается параболы в нижней точке) и $a=2$ (график пересекает прямую и параболу в разных точках)
Ответ: $a=-5$ и $a=2$

– три общие точки:
Прямая пересекает график в двух точках на параболе и одной на прямой. Это возможно, если $a\in (-5;0)$, так как для значений от -5 до 0 парабола принимает два значения, а прямая — одно.$$

Ответ: $a\in (-5;0)$

б) $y=\{\begin{array}{ll}x,& \text{если }x\le -1;\\ x^2-2,& \text{если }x>-1;\end{array}$

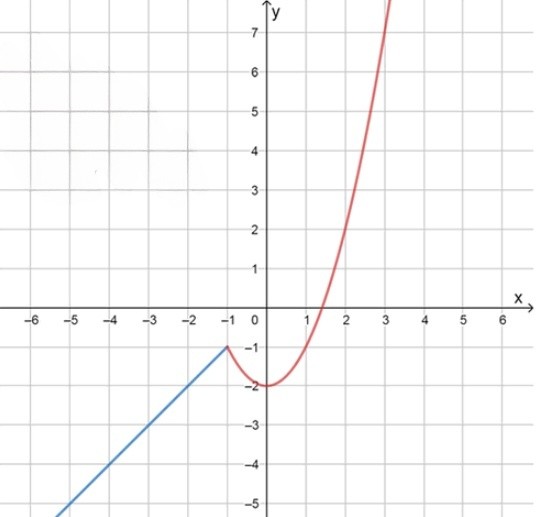
Первая часть — линейная функция $y=x$ при $x\le -1$. Таблица:

При $x=-2$, $y=-2$
При $x=-1$, $y=-1$

$\overline{)\begin{array}{ccc}x& -2& -1\\ y& -2& -1\end{array}}$

Вторая часть — парабола $y=x^2-2$, определена при $x>-1$. Вершина в точке $x=0$, $y=0^2-2=-2$. Таблица:

При $x=-1$, $y=(-1{)}^2-2=-1$
При $x=1$, $y=1^2-2=-1$
При $x=2$, $y=4-2=2$
При $x=3$, $y=9-2=7$

$\overline{)\begin{array}{ccccc}x& -1& 1& 2& 3\\ y& -1& -1& 2& 7\end{array}}$

График состоит из двух частей: прямая $y=x$, и парабола $y=x^2-2$. Прямая определена для $x\le -1$, парабола — для $x>-1$. В точке $x=-1$ обе части дают одно и то же значение $y=-1$, поэтому график непрерывен.

Определим, при каких значениях $a$ прямая $y=a$ имеет:

– одну общую точку:
Если $y=a$ пересекает только одну часть графика. Например, если $y=-3$, она пересечёт только прямую, так как парабола не достигает значений ниже -2. Или если $y=4$, она пересечёт только параболу.
Также одна точка будет, если прямая проходит через точку касания.
Ответ: $a\in (-\mathrm{\infty };-2)\cup (0;+\mathrm{\infty })\cup \{-2\}$

– две общие точки:
Если прямая проходит через общую границу обеих частей графика. Например, $y=-1$ пересекает прямую и параболу. Или если $y=-2$, она касается вершины параболы и идёт через прямую.
Ответ: $a=-1$

– три общие точки:
Прямая пересекает график в двух точках на параболе и одной на прямой. Это возможно, если $a\in (-2;-1)$.
Ответ: $a\in (-2;-1)$