
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Остальные Задания Для Старого Учебника(2019) Номер 331 Дорофеев, Суворова — Подробные Ответы
Постройте график функции и определите промежутки, на которых функция принимает положительные значения; отрицательные значения:
а)
б)
а)
— уравнение гиперболы:
— уравнение параболы:
и ;
— уравнение гиперболы:
График искомой функции:
Положительные значения при: ;
Отрицательные значения при: ;
б)
— уравнение прямой:
— уравнение параболы:
и ;
— уравнение прямой:
График искомой функции:
Положительные значения при: ;
Отрицательные значения при: ;
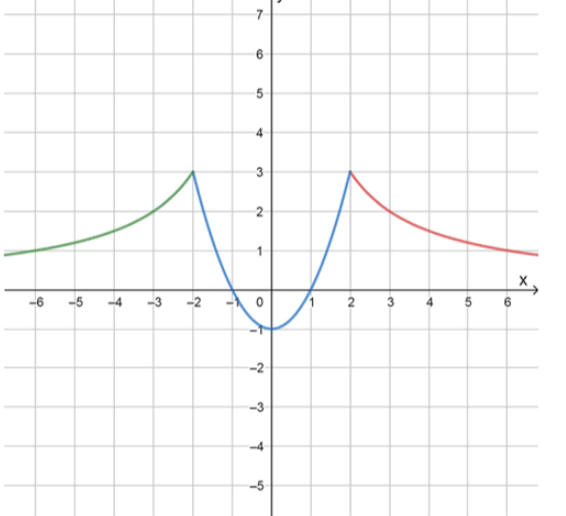
а)
Рассмотрим каждый участок функции по отдельности.
Первый участок: , при
Это гипербола с разрывом в точке , но нас интересует область . Выберем значения , большие 2, и подставим их в формулу.
При ,
При ,
При ,
Запишем значения в таблицу:
Второй участок: , при , то есть
Это уравнение параболы с вершиной в точке , так как , . Значения найдём по таблице:
При ,
При ,
При ,
При ,
Таблица:
Третий участок: , при
Это тоже гипербола, но с противоположным знаком.
При ,
При ,
При ,
Таблица:
Промежутки знакопостоянства функции:
Положительные значения функция принимает на тех промежутках, где значения . По таблицам видно:
При :
гипербола даёт положительные значения, потому что делим на отрицательное число (отрицательное на отрицательное даёт положительное)
При :
гипербола положительна, так как
Значит:
Положительные значения при
Отрицательные значения при , так как только в этом промежутке
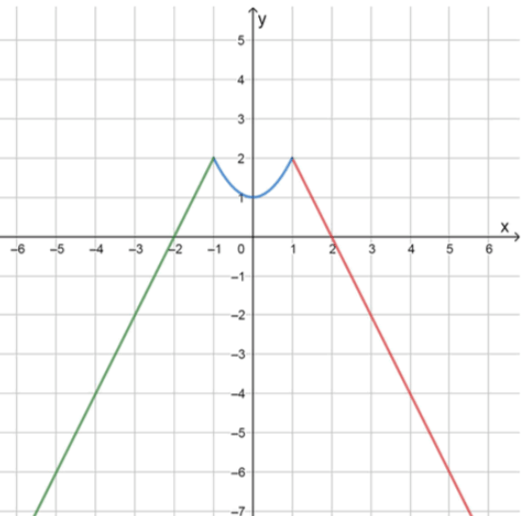
б)
Рассмотрим все три части функции.
Первый участок: , при
Это линейная функция с угловым коэффициентом .
При ,
При ,
Таблица:
Второй участок: , при
Это парабола, которая принимает наименьшее значение при :
При ,
При ,
Таблица:
Третий участок: , при
Это линейная функция с угловым коэффициентом
При ,
При ,
Таблица:
Анализируем знаки значений:
Положительные значения:
Парабола всегда положительна
Также выражение при , а при
Значит:
Положительные значения при
Отрицательные значения при




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!