ГДЗ по Алгебре 9 Класс Остальные Задания Для Старого Учебника(2019) Номер 328 Дорофеев, Суворова — Подробные Ответы

а) Постройте график функции $y=\frac{2x-x^2}{2x+4}$. Определите множество значений $x$, при которых значения функции отрицательны.
б) Постройте график функции $y=\frac{x^3-x^2-2x}{x-2}$. Определите множество значений $x$, при которых значения функции положительны.

а) $y=\frac{4x-x^3}{2x+4}$:

$y=\frac{x(4-x^2)}{2(x+2)}=\frac{x(2-x)(2+x)}{2(x+2)}=\frac{2x-x^2}{2}=x-\frac{1}{2}{x}^2;$

1) Имеет смысл при:
$2x+4\mathrm{\ne }0,$ отсюда $x\mathrm{\ne }-2;$

$\mathrm{2)\; y}\mathrm{\ne }-2-\frac{1}{2}\cdot 4\Rightarrow y\mathrm{\ne }-4;$

$\mathrm{3)\; y}=x-\frac{1}{2}{x}^2$ — уравнение параболы:
$x_0=-\frac{1}{2\cdot (-0.5)}=1$ и
$y_0=1-\frac{1}{2}\cdot 1^2=\frac{1}{2};$

Таблица значений:

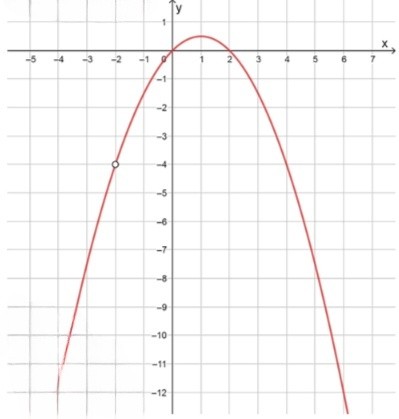
График искомой функции:

Значения отрицательны при:
$x\in (-\mathrm{\infty };-2)\cup (-2;0)\cup (2;+\mathrm{\infty })$

б) $y=\frac{x^3-x^2-2x}{x-2}$:

$y=\frac{x(x^2-x-2)}{x-2};$

1) Имеет смысл при:
$x-2\mathrm{\ne }0,$ отсюда $x\mathrm{\ne }2;$

2) Разложим на множители:
$x^2-x-2=0;$
$D=1^2+4\cdot 2=1+8=9,$ тогда:
$x_1=\frac{1-3}{2}=-1,x_2=\frac{1+3}{2}=2;$
$x^2-x-2=(x+1)(x-2);$

3) Получим функцию:
$y=\frac{x(x-2)(x+1)}{x-2}=x(x+1)=x^2+x;$

$\mathrm{4)\; y}\mathrm{\ne }{2}^2+2\Rightarrow y\mathrm{\ne }6;$

$\mathrm{5)\; y}=x^2+x$ — уравнение параболы:
$x_0=-\frac{1}{2},y_0={(-\frac{1}{2})}^2-\frac{1}{2}=\frac{1}{4}-\frac{1}{2}=-\frac{1}{2};$

Таблица значений:

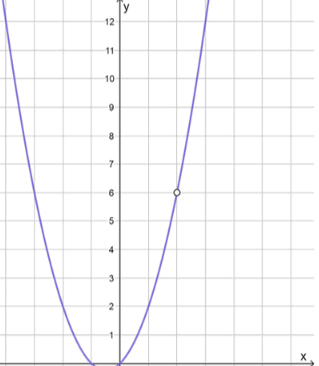
График искомой функции:

Значения положительны при:
$x\in (-\mathrm{\infty };-1)\cup (0;2)\cup (2;+\mathrm{\infty })$

а) $y=\frac{4x-x^3}{2x+4}$

Представим числитель в разложенном виде:
$y=\frac{4x-x^3}{2x+4}=\frac{-x^3+4x}{2x+4}$

Вынесем $x$ за скобки в числителе:
$y=\frac{x(-x^2+4)}{2(x+2)}$

Представим выражение $-x^2+4$ как разность квадратов:
$-x^2+4=-(x^2-4)=-(x-2)(x+2)$

Тогда:
$y=\frac{x\cdot (-(x-2)(x+2))}{2(x+2)}$

Сократим на $x+2$, если $x\mathrm{\ne }-2$:
$y=\frac{-x(x-2)}{2}=\frac{-x^2+2x}{2}=x-\frac{1}{2}{x}^2$

Область определения: знаменатель $2x+4\mathrm{\ne }0$, значит $x\mathrm{\ne }-2$

Проверим значение функции при $x=-2$:
подставим в выражение $y=x-\frac{1}{2}{x}^2$:
$y=-2-\frac{1}{2}\cdot 4=-2-2=-4$

Значит, функция не определена при $x=-2$, а также не принимает значения $y=-4$, т.к. при $x=-2$ возникает разрыв

Функция $y=x-\frac{1}{2}{x}^2$ — это квадратичная функция.
Стандартный вид: $y=-\frac{1}{2}{x}^2+x$

Найдём вершину параболы. Координата вершины по формуле:
$x_0=-\frac{b}{2a}=-\frac{1}{2\cdot (-\frac{1}{2})}=1$

Подставим в выражение:
$y_0=1-\frac{1}{2}\cdot 1^2=\frac{1}{2}$

Точка максимума: $(1,\frac{1}{2})$

Ветви параболы направлены вниз, так как коэффициент при $x^2$ отрицательный

Составим таблицу значений:

Промежутки знакоположительности и знакoотрицательности:
$y<0$ при $x\in (-\mathrm{\infty };-2)\cup (-2;0)\cup (2;+\mathrm{\infty })$
$y=0$ при $x=0$ и $x=2$
$y>0$ при $x\in (0;2)$

График имеет разрыв при $x=-2$ и удаляет значение $y=-4$

б) $y=\frac{x^3-x^2-2x}{x-2}$

Разложим числитель:
$x^3-x^2-2x=x(x^2-x-2)$

Разложим квадратный трёхчлен:
$x^2-x-2=(x-2)(x+1)$

Тогда:
$y=\frac{x(x-2)(x+1)}{x-2}$

Сократим на $x-2$, если $x\mathrm{\ne }2$:
$y=x(x+1)=x^2+x$

Область определения: $x\mathrm{\ne }2$

При $x=2$, значение функции должно быть:
$y=2^2+2=4+2=6$ — но оно исключается

Значит, $y\mathrm{\ne }6$

Функция $y=x^2+x$ — парабола с ветвями вверх
Вершина параболы:
$x_0=-\frac{1}{2}$
$y_0={(-\frac{1}{2})}^2+(-\frac{1}{2})=\frac{1}{4}-\frac{1}{2}=-\frac{1}{4}$

Составим таблицу значений:

Нули функции:
$x^2+x=0\Rightarrow x(x+1)=0\Rightarrow x=0,x=-1$

Промежутки знакоположительности:
$y>0$ при $x\in (-\mathrm{\infty };-1)\cup (0;2)\cup (2;+\mathrm{\infty })$

$y=0$ при $x=-1$ и $x=0$

$y<0$ при $x\in (-1;0)$

Разрыв в точке $x=2$, значение $y=6$ исключается из множества значений функции