ГДЗ по Алгебре 9 Класс Остальные Задания Для Старого Учебника(2019) Номер 312 Дорофеев, Суворова — Подробные Ответы

Решите неравенство:

а) $(x+1)(x-1)(2x-5)<0;$
б) $(x+4)(3x-9)?0;$
в) $x(2x-3)(x+5)>0;$
г) $(x-3)(3x-2)(x+2)?0.$

Подсказка. Преобразуйте неравенство в равносильное так, чтобы в каждом из множителей коэффициент при $x$ был равен 1. Например, а: вынесите в двучлене $2x-5$ множитель 2 за скобки и разделите обе части неравенства на 2.

а) $(x+1)(x-1)(2x-5)<0$;
$(x+1)(x-1)\cdot 2(x-2,5)<0\mathrm{\mid }:2$;
$(x+1)(x-1)(x-2,5)<0$;

1) Нули функции:
$x_1+1=0$, отсюда $x_1=-1$;
$x_2-1=0$, отсюда $x_2=1$;
$x_3-2,5=0$, отсюда $x_3=2,5$;

2) Значения на интервалах:

Ответ: $(-\mathrm{\infty };-1)\cup (1;2,5)$.

б) $(x+4)(3x-9)\le 0$;
$(x+4)\cdot 3(x-3)\le 0\mathrm{\mid }:3$;
$(x+4)(x-3)\le 0$;

1) Нули функции:
$x_1+4=0$, отсюда $x_1=-4$;
$x_2-3=0$, отсюда $x_2=3$;

2) Значения на интервалах:

Ответ: $[-4;3]$.

в) $x(2x-3)(x+5)>0$;
$x\cdot 2(x-1,5)(x+5)>0\mathrm{\mid }:2$;
$x(x-1,5)(x+5)>0$;

1) Нули функции:
$x_1=0$;
$x_2-1,5=0$, отсюда $x_2=1,5$;
$x_3+5=0$, отсюда $x_3=-5$;

2) Значения на интервалах:

Ответ: $(-5;0)\cup (1,5;+\mathrm{\infty })$.

г) $(x-3)(3x-2)(x+2)\ge 0$;
$(x-3)\cdot 3(x-\frac{2}{3})(x+2)\ge 0\mathrm{\mid }:3$;
$(x-3)(x-\frac{2}{3})(x+2)\ge 0$;

1) Нули функции:
$x_1-3=0$, отсюда $x_1=3$;
$x_2-\frac{2}{3}=0$, отсюда $x_2=\frac{2}{3}$;
$x_3+2=0$, отсюда $x_3=-2$;

2) Значения на интервалах:

Ответ: $[-2;\frac{2}{3}]\cup [3;+\mathrm{\infty })$.

а) Начальное неравенство: $(x+1)(x-1)(2x-5)<0$. Здесь присутствует множитель $2x-5$, у которого коэффициент перед $x$ равен 2, поэтому для приведения коэффициента к единице выносим 2 за скобку: $(x+1)(x-1)\cdot 2(x-2,5)<0$. Далее делим обе части неравенства на положительное число 2, знак неравенства при этом не изменяется: $(x+1)(x-1)(x-2,5)<0$.

Теперь находим нули функции. Для этого приравниваем каждый множитель к нулю:

$x+1=0\Rightarrow x=-1$.

$x-1=0\Rightarrow x=1$.

$x-2,5=0\Rightarrow x=2,5$.

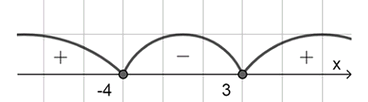
Таким образом, критические точки равны $x=-1$, $x=1$, $x=2,5$. Эти точки делят числовую ось на четыре промежутка: $(-\mathrm{\infty };-1)$, $(-1;1)$, $(1;2,5)$, $(2,5;+\mathrm{\infty })$. Для каждого промежутка определим знак произведения трёх множителей.

На интервале $(-\mathrm{\infty };-1)$: берём точку $x=-2$. Тогда $(-2+1)(-2-1)(-2-2,5)=(-1)(-3)(-4,5)=-13,5<0$. Знак отрицательный, условие выполняется.
На интервале $(-1;1)$: берём точку $x=0$. Тогда $(0+1)(0-1)(0-2,5)=(1)(-1)(-2,5)=2,5>0$. Знак положительный, условие не выполняется.
На интервале $(1;2,5)$: берём точку $x=2$. Тогда $(2+1)(2-1)(2-2,5)=(3)(1)(-0,5)=-1,5<0$. Знак отрицательный, условие выполняется.
На интервале $(2,5;+\mathrm{\infty })$: берём точку $x=3$. Тогда $(3+1)(3-1)(3-2,5)=(4)(2)(0,5)=4>0$. Знак положительный, условие не выполняется.

Итог: решение $(-\mathrm{\infty };-1)\cup (1;2,5)$.

б) Начальное неравенство: $(x+4)(3x-9)\le 0$. Здесь множитель $3x-9$ имеет коэффициент 3 перед $x$, поэтому выносим 3 за скобку: $(x+4)\cdot 3(x-3)\le 0$. Делим обе части на положительное число 3, знак сохраняется: $(x+4)(x-3)\le 0$.

Находим нули функции:

$x+4=0\Rightarrow x=-4$.

$x-3=0\Rightarrow x=3$.

Точки $x=-4$ и $x=3$ делят ось на интервалы: $(-\mathrm{\infty };-4)$, $(-4;3)$, $(3;+\mathrm{\infty })$.

На интервале $(-\mathrm{\infty };-4)$: берём $x=-5$. Тогда $(-5+4)(-5-3)=(-1)(-8)=8>0$. Знак положительный, условие не выполняется.
На интервале $(-4;3)$: берём $x=0$. Тогда $(0+4)(0-3)=(4)(-3)=-12<0$. Знак отрицательный, условие выполняется.
На интервале $(3;+\mathrm{\infty })$: берём $x=4$. Тогда $(4+4)(4-3)=(8)(1)=8>0$. Знак положительный, условие не выполняется.

Так как неравенство неп strictое ($\le 0$), включаем точки $x=-4$ и $x=3$. Итог: $[-4;3]$.

в) Начальное неравенство: $x(2x-3)(x+5)>0$. Множитель $2x-3$ содержит коэффициент 2 перед $x$. Вынесем 2: $x\cdot 2(x-1,5)(x+5)>0$. Делим обе части на положительное число 2, знак неравенства сохраняется: $x(x-1,5)(x+5)>0$.

Нули функции:

$x=0$.

$x-1,5=0\Rightarrow x=1,5$.

$x+5=0\Rightarrow x=-5$.

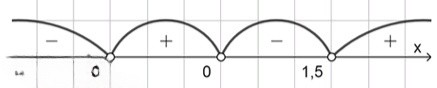
Критические точки: $-5,0,1,5$. Интервалы: $(-\mathrm{\infty };-5)$, $(-5;0)$, $(0;1,5)$, $(1,5;+\mathrm{\infty })$.

На интервале $(-\mathrm{\infty };-5)$: берём $x=-6$. Тогда $(-6)(-6-1,5)(-6+5)=(-6)(-7,5)(-1)=-45<0$. Условие не выполняется.
На интервале $(-5;0)$: берём $x=-1$. Тогда $(-1)(-1-1,5)(-1+5)=(-1)(-2,5)(4)=10>0$. Условие выполняется.
На интервале $(0;1,5)$: берём $x=1$. Тогда $(1)(1-1,5)(1+5)=(1)(-0,5)(6)=-3<0$. Условие не выполняется.
На интервале $(1,5;+\mathrm{\infty })$: берём $x=2$. Тогда $(2)(2-1,5)(2+5)=(2)(0,5)(7)=7>0$. Условие выполняется.

Итог: решение $(-5;0)\cup (1,5;+\mathrm{\infty })$.

г) Начальное неравенство: $(x-3)(3x-2)(x+2)\ge 0$. Вынесем коэффициент 3 из второго множителя: $(x-3)\cdot 3(x-\frac{2}{3})(x+2)\ge 0$. Делим обе части на положительное число 3, знак сохраняется: $(x-3)(x-\frac{2}{3})(x+2)\ge 0$.

Нули функции:

$x-3=0\Rightarrow x=3$.

$x-\frac{2}{3}=0\Rightarrow x=\frac{2}{3}$.

$x+2=0\Rightarrow x=-2$.

Интервалы: $(-\mathrm{\infty };-2)$, $(-2;\frac{2}{3})$, $(\frac{2}{3};3)$, $(3;+\mathrm{\infty })$.

На интервале $(-\mathrm{\infty };-2)$: берём $x=-3$. Тогда $(-3-3)(-3-\frac{2}{3})(-3+2)=(-6)(-3,67)(-1)=-22,02<0$. Условие не выполняется.
На интервале $(-2;\frac{2}{3})$: берём $x=0$. Тогда $(0-3)(0-\frac{2}{3})(0+2)=(-3)(-0,67)(2)=4>0$. Условие выполняется.
На интервале $(\frac{2}{3};3)$: берём $x=1$. Тогда $(1-3)(1-0,67)(1+2)=(-2)(0,33)(3)=-2<0$. Условие не выполняется.
На интервале $(3;+\mathrm{\infty })$: берём $x=4$. Тогда $(4-3)(4-0,67)(4+2)=(1)(3,33)(6)=19,98>0$. Условие выполняется.

Так как знак $\ge 0$, включаем нули функции: $-2,\frac{2}{3},3$.

Итог: решение $[-2;\frac{2}{3}]\cup [3;+\mathrm{\infty })$.