ГДЗ по Алгебре 9 Класс Остальные Задания Для Старого Учебника(2019) Номер 311 Дорофеев, Суворова — Подробные Ответы

Решите неравенство методом интервалов:
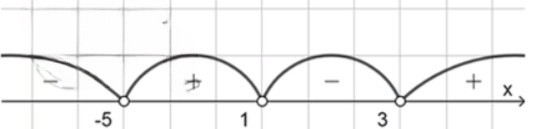
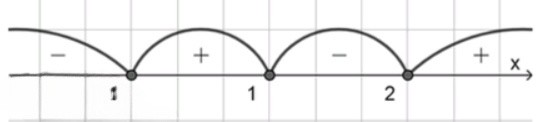
а) (x + 5)(х — 3)(х — 1) > 0; в) (х — 1)(х + 2)(х — 2) ⩽ 0;
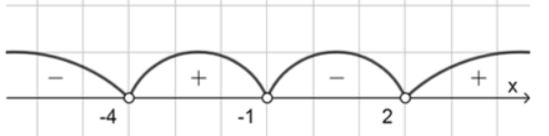
б) (х — 2)(х + 4)(х + 1) < 0; г) х(х + 3)(х — 5) ⩾ 0.
Подсказка. Отметив корни на координатной прямой, запишите неравенство, расположив множители в порядке возрастания корней. Пункты в) и г): обратите внимание на то, что значения х, которые обращают произведение в нуль, входят в множество решений неравенства; чтобы не забыть об этом, на координатной прямой отмечайте точки чёрным кружком.

а) $(x+5)(x-3)(x-1)>0$;

1) Нули функции:
$x_1+5=0$, отсюда $x_1=-5$;
$x_2-3=0$, отсюда $x_2=3$;
$x_3-1=0$, отсюда $x_3=1$;

2) Значения на интервалах:

$(x+5)(x-1)(x-3)>0$;

Ответ: $(-5;1)\cup (3;+\mathrm{\infty })$.

б) $(x-2)(x+4)(x+1)<0$;

1) Нули функции:
$x_1-2=0$, отсюда $x_1=2$;
$x_2+4=0$, отсюда $x_2=-4$;
$x_3+1=0$, отсюда $x_3=-1$;

2) Значения на интервалах:

$(x+4)(x+1)(x-2)<0$;

Ответ: $(-\mathrm{\infty };-4)\cup (-1;2)$.

в) $(x-1)(x+2)(x-2)⩽0$;

1) Нули функции:
$x_1-1=0$, отсюда $x_1=1$;
$x_2+2=0$, отсюда $x_2=-2$;
$x_3-2=0$, отсюда $x_3=2$;

2) Значения на интервалах:

$(x+2)(x-1)(x-2)⩽0$;

Ответ: $(-\mathrm{\infty };-2]\cup [1;2]$.

г) $x(x+3)(x-5)\ge 0$;

1) Нули функции:
$x_1=0$;
$x_2+3=0$, отсюда $x_2=-3$;
$x_3-5=0$, отсюда $x_3=5$;

2) Значения на интервалах:

$(x+3)\cdot x\cdot (x-5)⩾0$;

Ответ: $[-3;0]\cup [5;+\mathrm{\infty })$.

а) $(x+5)(x-3)(x-1)>0$;

Нули функции: из $x+5=0$ получаем $x=-5$; из $x-3=0$ получаем $x=3$; из $x-1=0$ получаем $x=1$.

Упорядочим корни по возрастанию: $-5<1<3$. Все корни простые (кратность $1$), значит при прохождении через каждый из них знак произведения меняется.

Степень произведения равна $3$ (нечётная), старший коэффициент положителен, поэтому при $x\to -\mathrm{\infty }$ значение $(x+5)(x-3)(x-1)<0$, а при $x\to +\mathrm{\infty }$ значение $>0$.

Разбиваем ось на интервалы $(-\mathrm{\infty };-5)$, $(-5;1)$, $(1;3)$, $(3;+\mathrm{\infty })$ и проверяем знак на каждом (достаточно одной точки внутри интервала): для $x=-6$ получаем $(-1)\cdot (-9)\cdot (-7)<0$; для $x=0$ получаем $5\cdot (-3)\cdot (-1)>0$; для $x=2$ получаем $7\cdot (-1)\cdot 1<0$; для $x=4$ получаем $9\cdot 1\cdot 3>0$.

Требуется $>0$: берём интервалы со знаком $>0$; точки $x=-5$, $x=1$, $x=3$ не включаем из-за строгости.

Ответ: $(-5;1)\cup (3;+\mathrm{\infty })$.

б) $(x-2)(x+4)(x+1)<0$;

Нули функции: из $x-2=0$ получаем $x=2$; из $x+4=0$ получаем $x=-4$; из $x+1=0$ получаем $x=-1$.

Упорядочим корни: $-4<-1<2$. Все корни простые, знак меняется при каждом корне.

Степень $3$, старший коэффициент положителен: при $x\to -\mathrm{\infty }$ знак $<0$, при $x\to +\mathrm{\infty }$ знак $>0$.

Интервалы $(-\mathrm{\infty };-4)$, $(-4;-1)$, $(-1;2)$, $(2;+\mathrm{\infty })$. Проверяем: для $x=-5$ получаем $(-7)\cdot (-1)\cdot (-4)<0$; для $x=-2$ получаем $(-4)\cdot 2\cdot (-1)>0$; для $x=0$ получаем $(-2)\cdot 4\cdot 1<0$; для $x=3$ получаем $1\cdot 7\cdot 4>0$.

Требуется $<0$: берём интервалы со знаком $<0$, корни не включаем.

Ответ: $(-\mathrm{\infty };-4)\cup (-1;2)$.

в) $(x-1)(x+2)(x-2)⩽0$;

Нули функции: из $x-1=0$ получаем $x=1$; из $x+2=0$ получаем $x=-2$; из $x-2=0$ получаем $x=2$.

Упорядочим корни: $-2<1<2$. Все корни простые, знак меняется на каждом.

Степень $3$, старший коэффициент положителен: при $x\to -\mathrm{\infty }$ знак $<0$, при $x\to +\mathrm{\infty }$ знак $>0$.

Интервалы $(-\mathrm{\infty };-2)$, $(-2;1)$, $(1;2)$, $(2;+\mathrm{\infty })$. Проверяем: для $x=-3$ получаем $(-4)\cdot (-1)\cdot (-5)<0$; для $x=0$ получаем $(-1)\cdot 2\cdot (-2)>0$; для $x=\mathrm{1,5}$ получаем $\mathrm{0,5}\cdot \mathrm{3,5}\cdot (-\mathrm{0,5})<0$; для $x=3$ получаем $2\cdot 5\cdot 1>0$.

Требуется $⩽0$: берём интервалы со знаком $<0$ и добавляем корни, где значение $=0$, то есть $x=-2$, $x=1$, $x=2$.

Ответ: $(-\mathrm{\infty };-2]\cup [1;2]$.

г) $x(x+3)(x-5)⩾0$;

Нули функции: из $x=0$ получаем $x=0$; из $x+3=0$ получаем $x=-3$; из $x-5=0$ получаем $x=5$.

Упорядочим корни: $-3<0<5$. Все корни простые, знак меняется при каждом.

Степень $3$, старший коэффициент положителен: при $x\to -\mathrm{\infty }$ знак $<0$, при $x\to +\mathrm{\infty }$ знак $>0$.

Интервалы $(-\mathrm{\infty };-3)$, $(-3;0)$, $(0;5)$, $(5;+\mathrm{\infty })$. Проверяем: для $x=-4$ получаем $(-4)\cdot (-1)\cdot (-9)<0$; для $x=-1$ получаем $(-1)\cdot 2\cdot (-6)>0$; для $x=2$ получаем $2\cdot 5\cdot (-3)<0$; для $x=6$ получаем $6\cdot 9\cdot 1>0$.

Требуется $⩾0$: берём интервалы со знаком $>0$ и включаем точки нулей, где значение $=0$, то есть $x=-3$, $x=0$, $x=5$.

Ответ: $[-3;0]\cup [5;+\mathrm{\infty })$.