ГДЗ по Алгебре 9 Класс Остальные Задания Для Старого Учебника(2019) Номер 178 Дорофеев, Суворова — Подробные Ответы

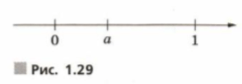
На координатной прямой отмечено число $a$ (рис. 1.29). Расположите в порядке возрастания числа $a$, $\frac{1}{a}$ и $a^2$.

1) По рисунку определим, что: $0<a<1$;

$\mathrm{2)\; a}<1$, значит $a-1<0$ и $1-a>0$;

${\mathrm{3)\; a}}^2-a=a(a-1)$;

$a>0$ и $a-1<0$, значит $a^2-a<0$, тогда $a^2<a$;

4) $\frac{1}{a}-1=\frac{1-a}{a}$;$\frac{\mathrm{}}{}$

$a>0$ и $1-a>0$, значит $\frac{1}{a}-1>0$, тогда $\frac{1}{a}>1>a$;

Ответ: $a^2$; $a$; $\frac{1}{a}$.

По рисунку определим, что $0<a<1$. Это означает, что $a$ — положительное число, которое меньше единицы. Такое положение числа на координатной прямой позволяет нам сделать определенные выводы о его свойствах.

$a<1$, значит $a-1<0$ и $1-a>0$. Это следует из простых свойств неравенств. Если $a$ меньше 1, то $a-1$ обязательно будет отрицательным, а $1-a$ — положительным. Это важно для дальнейших шагов.

$a^2-a=a(a-1)$. Это представление числа $a^2-a$ в виде произведения, где $a$ — общий множитель. Умножив $a$ на $(a-1)$, получаем тот же результат, что и при разложении выражения $a^2-a$. Давайте проанализируем знаки этого произведения.

$a>0$ и $a-1<0$, значит $a^2-a<0$, тогда $a^2<a$. Если $a$ положительно, но меньше единицы, то $a-1$ отрицательно, и, следовательно, произведение $a(a-1)$ также будет отрицательным. То есть $a^2-a<0$, а следовательно, $a^2<a$. Это показывает, что для чисел в интервале $(0,1)$, квадрат числа всегда меньше самого числа.

$\frac{1}{a}-1=\frac{1-a}{a}$. Это преобразование дробного выражения в более удобную для анализа форму. Здесь мы просто привели к общему знаменателю.

$a>0$ и $1-a>0$, значит $\frac{1}{a}-1>0$, тогда $\frac{1}{a}>1>a$. Поскольку $1-a$ положительно, это означает, что $\frac{1}{a}-1$ также положительно. То есть $\frac{1}{a}>1$. Так как $a$ меньше единицы, то $\frac{1}{a}$ всегда больше 1, а сам $a$ — меньше 1.

Ответ: $a^2$; $a$; $\frac{1}{a}$.