ГДЗ по Алгебре 9 Класс Остальные Задания Для Старого Учебника(2019) Номер 138 Дорофеев, Суворова — Подробные Ответы

Проиллюстрируйте геометрически следующий факт: если $a$ и $b$ — положительные числа, то $a^3>b^3$ в том и только в том случае, когда $a>b$. Докажите этот факт алгебраически.

Доказать: если $a$ и $b$ — положительные числа, то $a^3>b^3$ в том и только в том случае, если $a>b$;

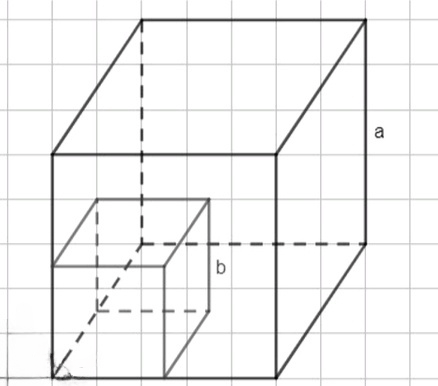
1)Проиллюстрируем данный факт геометрически:

Объемы кубов со сторонами $a$ и $b$ равны $a^3$ и $b^3$ соответственно;

2)Докажем, что если $a>b>0$, тогда $a^3>b^3$:

$$a^3-b^3=(a-b)(a^2+ab+b^2)$$

Так как $a>b>0$, то $a-b>0$ и $a^2+ab+b^2>0$;
Тогда:

$$a^3-b^3>0$$

Отсюда:

$$a^3>b^3$$

3)Докажем, что если $a^3>b^3$, $a>0$ и $b>0$, тогда $a>b$:
Из $a^3>b^3$ получаем:

$$a^3-b^3>0$$$$(a-b)(a^2+ab+b^2)>0$$

Так как $a>0$ и $b>0$, то $(a^2+ab+b^2)>0$;
Тогда:

$$(a-b)>0$$

Отсюда:

$$a>b$$

Доказать: если $a$ и $b$ — положительные числа, то $a^3>b^3$ в том и только в том случае, если $a>b$;

1)Проиллюстрируем данный факт геометрически:
Объемы кубов со сторонами $a$ и $b$ равны $a^3$ и $b^3$ соответственно. Так как объем куба увеличивается с увеличением длины его стороны, то, если $a>b$, то и объем куба со стороной $a$ будет больше, чем объем куба со стороной $b$. Следовательно, если $a>b$, то $a^3>b^3$.

2)Докажем, что если $a>b>0$, то $a^3>b^3$:

Рассмотрим разность $a^3-b^3$:

$$a^3-b^3=(a-b)(a^2+ab+b^2)$$

Это разложение использует формулу разности кубов. Теперь рассмотрим каждый множитель по отдельности.

• $a-b>0$, так как $a>b>0$.
• $a^2+ab+b^2$ — это сумма положительных чисел. Ведь все слагаемые в этой сумме положительны, так как $a>0$ и $b>0$.

Таким образом, оба множителя $(a-b)$ и $(a^2+ab+b^2)$ положительные, следовательно, их произведение:

$$a^3-b^3=(a-b)(a^2+ab+b^2)>0$$

Следовательно:

$$a^3>b^3$$

что и требовалось доказать.

3)Докажем, что если $a^3>b^3$, $a>0$ и $b>0$, то $a>b$:

Из $a^3>b^3$ получаем:

$$a^3-b^3>0$$

Теперь раскроем разность кубов:

$$(a-b)(a^2+ab+b^2)>0$$

Сначала рассмотрим множитель $(a-b)$:

Если $a>b$, то $a-b>0$.

Теперь рассмотрим второй множитель $a^2+ab+b^2$:

Поскольку $a$ и $b$ — положительные числа, то каждый из членов в выражении $a^2+ab+b^2$ положителен:

$a^2>0$,

$ab>0$,

$b^2>0$.

Следовательно, $a^2+ab+b^2>0$. Таким образом, оба множителя $(a-b)$ и $(a^2+ab+b^2)$ положительные, что означает, что:

$$(a-b)(a^2+ab+b^2)>0$$

И, следовательно:

$$a-b>0$$

Отсюда $a>b$, что и требовалось доказать.