ГДЗ по Алгебре 9 Класс Номер 718 Дорофеев, Суворова — Подробные Ответы

Существует формула, по которой биномиальные коэффициенты можно вычислять непосредственно, не прибегая к треугольнику Паскаля:

$C_n^m=\frac{n!}{m!(n-m)!}$.

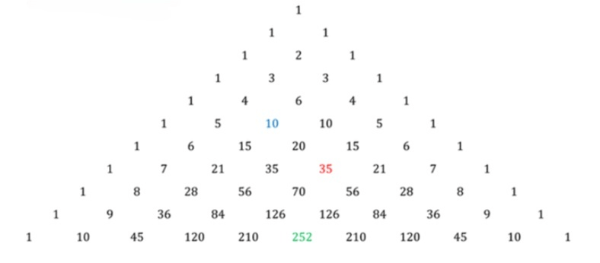
1) Найдите по формуле $C_7^4$; $C_5^2$; $C_{10}^5$. Сравните с результатом, полученным с помощью треугольника Паскаля.

2) Докажите, что $C_{12}^4=C_{12}^8$.

3) Докажите, что $C_7^2+C_7^3=C_8^3$.

4) Докажите, что $C_n^m+C_n^{m+1}=C_{n+1}^{m+1}$.

Формула значения биномиального коэффициента:

$C_n^m=\frac{n!}{m!(n-m)!}$;

1) Искомые коэффициенты:

$C_7^4=\frac{7!}{4!\cdot (7-4)!}=\frac{7!}{4!\cdot 3!}=\frac{7\cdot 6\cdot 5\cdot 4!}{4!\cdot 3\cdot 2\cdot 1}=\frac{210}{6}=35$;

$C_5^2=\frac{5!}{2!\cdot (5-2)!}=\frac{5!}{2!\cdot 3!}=\frac{5\cdot 4\cdot 3!}{2\cdot 1\cdot 3!}=\frac{20}{2}=10$;

$C_{10}^5=\frac{10!}{5!\cdot (10-5)!}=\frac{10!}{5!\cdot 5!}=\frac{10\cdot 9\cdot 8\cdot 7\cdot 6\cdot 5!}{5\cdot 4\cdot 3\cdot 2\cdot 1\cdot 5!}=2\cdot 3\cdot 2\cdot 7\cdot 3=252$;

Значения совпадают с результатом, полученным с помощью треугольника Паскаля:

${\mathrm{2)\; C}}_{12}^4=\frac{12!}{4!\cdot (12-4)!}=\frac{12!}{4!\cdot 8!}$;

$C_{12}^8=\frac{12!}{8!\cdot (12-8)!}=\frac{12!}{8!\cdot 4!}$;

$C_{12}^4=C_{12}^8$;

${\mathrm{3)\; C}}_7^2=\frac{7!}{2!\cdot (7-2)!}=\frac{7!}{2!\cdot 5!}=\frac{7\cdot 6\cdot 5!}{2\cdot 1\cdot 5!}=\frac{42}{2}=21$;

$C_7^3=\frac{7!}{3!\cdot (7-3)!}=\frac{7!}{3!\cdot 4!}=\frac{7\cdot 6\cdot 5\cdot 4!}{3\cdot 2\cdot 1\cdot 4!}=\frac{210}{6}=35$;

$C_8^3=\frac{8!}{3!\cdot (8-3)!}=\frac{8!}{3!\cdot 5!}=\frac{8\cdot 7\cdot 6\cdot 5!}{3\cdot 2\cdot 1\cdot 5!}=\frac{336}{6}=56$;

$C_7^2+C_7^3=21+35=56=C_8^3$;

${\mathrm{4)\; C}}_n^m+C_n^{m+1}=\frac{n!}{m!(n-m)!}+\frac{n!}{(m+1)!(n-m-1)!}=$

$=\frac{1}{n-m}\cdot \frac{n!}{m!(n-m-1)!}+\frac{1}{m+1}\cdot \frac{n!}{m!(n-m-1)!}=$

$=\frac{n!}{m!(n-m-1)!}\cdot (\frac{1}{n-m}+\frac{1}{m+1})=$

$=\frac{n!}{m!(n-m-1)!}\cdot \frac{m+1+n-m}{(n-m)(m+1)}=$

$=\frac{n!\cdot (n+1)}{m!\cdot (m+1)\cdot (n-m-1)!\cdot (n-m)}=\frac{(n+1)!}{(m+1)!\cdot (n-m)!}$;

$C_{n+1}^{m+1}=\frac{(n+1)!}{(m+1)!\cdot (n+1-m-1)!}=\frac{(n+1)!}{(m+1)!\cdot (n-m)!}$;

Формула значения биномиального коэффициента:

$C_n^m=\frac{n!}{m!(n-m)!}$.

Искомые коэффициенты.

Сначала найдём $C_7^4$. По формуле:
$C_7^4=\frac{7!}{4!(7-4)!}=\frac{7!}{4!\cdot 3!}$.

Факториал $7!=7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1$. Но при вычислении коэффициента удобно сокращать одинаковые множители сверху и снизу. Запишем:
$\frac{7!}{4!\cdot 3!}=\frac{7\cdot 6\cdot 5\cdot 4!}{4!\cdot 3!}$.

Сокращаем $4!$:
$\frac{7\cdot 6\cdot 5}{3!}=\frac{7\cdot 6\cdot 5}{3\cdot 2\cdot 1}=\frac{210}{6}=35$.

Теперь найдём $C_5^2$.
По формуле:
$C_5^2=\frac{5!}{2!(5-2)!}=\frac{5!}{2!\cdot 3!}$.

Разложим числитель:
$\frac{5\cdot 4\cdot 3!}{2!\cdot 3!}$.

Сокращаем $3!$:
$\frac{5\cdot 4}{2!}=\frac{20}{2}=10$.

Теперь найдём $C_{10}^5$.
По формуле:
$C_{10}^5=\frac{10!}{5!(10-5)!}=\frac{10!}{5!\cdot 5!}$.

Разложим:
$\frac{10\cdot 9\cdot 8\cdot 7\cdot 6\cdot 5!}{5!\cdot 5!}$.

Сокращаем $5!$:
$\frac{10\cdot 9\cdot 8\cdot 7\cdot 6}{5!}=\frac{30240}{120}=252$.

Итак:
$C_7^4=35$, $C_5^2=10$, $C_{10}^5=252$.

Проверка через треугольник Паскаля даёт те же самые значения.

Докажем равенство $C_{12}^4=C_{12}^8$.

По формуле:
$C_{12}^4=\frac{12!}{4!(12-4)!}=\frac{12!}{4!\cdot 8!}$.

Аналогично:
$C_{12}^8=\frac{12!}{8!(12-8)!}=\frac{12!}{8!\cdot 4!}$.

Обе дроби имеют одинаковый вид: $\frac{12!}{4!\cdot 8!}$.

Следовательно, $C_{12}^4=C_{12}^8$.

Это отражает симметрию биномиальных коэффициентов: $C_n^m=C_n^{n-m}$.

Докажем равенство $C_7^2+C_7^3=C_8^3$.

Сначала вычислим $C_7^2$.
$C_7^2=\frac{7!}{2!(7-2)!}=\frac{7!}{2!\cdot 5!}$.

Разложим:
$\frac{7\cdot 6\cdot 5!}{2\cdot 1\cdot 5!}=\frac{42}{2}=21$.

Теперь $C_7^3$.
$C_7^3=\frac{7!}{3!(7-3)!}=\frac{7!}{3!\cdot 4!}$.

Разложим:
$\frac{7\cdot 6\cdot 5\cdot 4!}{3\cdot 2\cdot 1\cdot 4!}=\frac{210}{6}=35$.

Теперь сложим:
$C_7^2+C_7^3=21+35=56$.

Найдём $C_8^3$:
$C_8^3=\frac{8!}{3!(8-3)!}=\frac{8!}{3!\cdot 5!}$.

Разложим:
$\frac{8\cdot 7\cdot 6\cdot 5!}{3\cdot 2\cdot 1\cdot 5!}=\frac{336}{6}=56$.

Таким образом, $C_7^2+C_7^3=C_8^3$.

Докажем равенство $C_n^m+C_n^{m+1}=C_{n+1}^{m+1}$.

Запишем левую часть:
$C_n^m=\frac{n!}{m!(n-m)!}$,
$C_n^{m+1}=\frac{n!}{(m+1)!(n-m-1)!}$.

Сложим:
$C_n^m+C_n^{m+1}=\frac{n!}{m!(n-m)!}+\frac{n!}{(m+1)!(n-m-1)!}$.

Приведём к общему виду. Первую дробь можно переписать так:
$\frac{n!}{m!(n-m)!}=\frac{1}{n-m}\cdot \frac{n!}{m!(n-m-1)!}$.

Вторая дробь:
$\frac{n!}{(m+1)!(n-m-1)!}=\frac{1}{m+1}\cdot \frac{n!}{m!(n-m-1)!}$.

Складываем:
$\frac{n!}{m!(n-m-1)!}(\frac{1}{n-m}+\frac{1}{m+1})$.

В скобках:
$\frac{1}{n-m}+\frac{1}{m+1}=\frac{m+1+n-m}{(n-m)(m+1)}=\frac{n+1}{(n-m)(m+1)}$.

Подставим:
$\frac{n!}{m!(n-m-1)!}\cdot \frac{n+1}{(n-m)(m+1)}$.

Заметим, что $(n-m)(n-m-1)!=(n-m)!$.

Тогда:
$\frac{n!\cdot (n+1)}{m!(m+1)(n-m)!}=\frac{(n+1)!}{(m+1)!(n-m)!}$.

Это именно формула для $C_{n+1}^{m+1}$.

Таким образом, доказано:
$C_n^m+C_n^{m+1}=C_{n+1}^{m+1}$.