ГДЗ по Алгебре 9 Класс Номер 714 Дорофеев, Суворова — Подробные Ответы

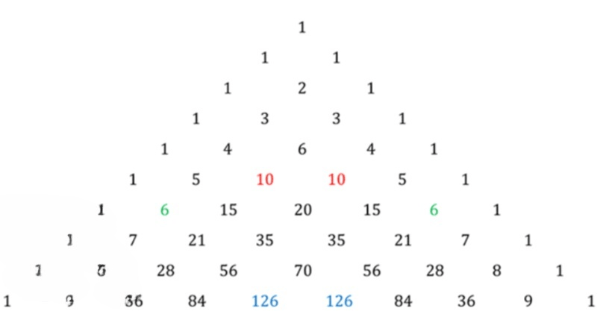
Сравните $C_5^2$ и $C_5^3$; $C_6^1$ и $C_6^5$; $C_9^4$ и $C_9^5$. Сформулируйте соответствующее свойство и запишите его в символическом виде.

1) Сравним данные элементы треугольника Паскаля:
$C_5^2 = 10$ и $C_5^3 = 10$, значит $C_5^2 = C_5^3$;
$C_6^1 = 6$ и $C_6^5 = 6$, значит $C_6^1 = C_6^5$;
$C_9^4 = 126$ и $C_9^5 = 126$, значит $C_9^4 = C_9^5$;

2) Сформулируем свойство:
Если у одного из двух элементов треугольника Паскаля, находящихся в одной строке, номер равен разности номера строки и номера второго элемента, то эти элементы равны: $C_n^m = C_n^{n-m}$;

1) Сравним данные элементы треугольника Паскаля подробно и с максимальной детализацией.

Для начала вспомним, что элементы треугольника Паскаля вычисляются по формуле $C_n^m = \frac{n!}{m! \cdot (n-m)!}$, где $n!$ — факториал числа $n$.

Сравнение $C_5^2$ и $C_5^3$:
Вычислим $C_5^2 = \frac{5!}{2! \cdot (5-2)!} = \frac{120}{2 \cdot 6} = \frac{120}{12} = 10$.
Вычислим $C_5^3 = \frac{5!}{3! \cdot (5-3)!} = \frac{120}{6 \cdot 2} = \frac{120}{12} = 10$.
Сравнивая результаты, получаем $C_5^2 = C_5^3 = 10$. Это показывает, что элементы с номерами $m$ и $n-m$ в одной строке всегда равны.

Сравнение $C_6^1$ и $C_6^5$:
Вычислим $C_6^1 = \frac{6!}{1! \cdot 5!} = \frac{720}{1 \cdot 120} = 6$.
Вычислим $C_6^5 = \frac{6!}{5! \cdot 1!} = \frac{720}{120 \cdot 1} = 6$.
Сравнивая, видим $C_6^1 = C_6^5 = 6$, подтверждая, что элементы симметричны относительно середины строки.

Сравнение $C_9^4$ и $C_9^5$:
Вычислим $C_9^4 = \frac{9!}{4! \cdot 5!} = \frac{362880}{24 \cdot 120} = \frac{362880}{2880} = 126$.
Вычислим $C_9^5 = \frac{9!}{5! \cdot 4!} = \frac{362880}{120 \cdot 24} = \frac{362880}{2880} = 126$.
Таким образом, $C_9^4 = C_9^5 = 126$.

2) Сформулируем свойство треугольника Паскаля:
Для любой строки с номером $n$ элементы, стоящие на позициях $m$ и $n-m$, равны: $C_n^m = C_n^{n-m}$.
Это свойство отражает полную симметрию треугольника Паскаля относительно вертикальной оси, проходящей через середину строки.

Пример расположения элементов для наглядности: