ГДЗ по Алгебре 9 Класс Номер 713 Дорофеев, Суворова — Подробные Ответы

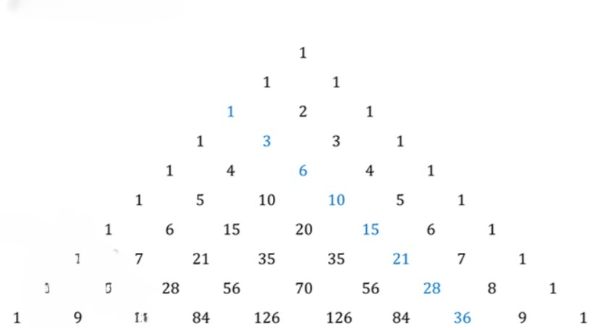
а) Запишите с помощью символа $C_n^m$ шестую и седьмую строки треугольника Паскаля.
б) Запишите с помощью символа $C_n^m$ несколько элементов какой-нибудь «диагонали» треугольника Паскаля.

а) Элементы треугольника Паскаля:

1) Шестая строка:
$C_6^0, C_6^1, C_6^2, C_6^3, C_6^4, C_6^5, C_6^6$;

2) Седьмая строка:
$C_7^0, C_7^1, C_7^2, C_7^3, C_7^4, C_7^5, C_7^6, C_7^7$;

б) Диагональ треугольных чисел:
$C_2^0, C_3^1, C_4^2, C_5^3, C_6^4, C_7^5, C_8^6, C_9^7, \ldots, C_{n+1}^{m-1}$;

Элементы треугольника Паскаля представляют собой биномиальные коэффициенты $C_n^m$, где $n$ — номер строки, а $m$ — номер элемента в строке, начиная с нуля. Каждая строка состоит из $n+1$ элементов, первый и последний элемент всегда равны $1$, а каждый внутренний элемент равен сумме двух элементов из предыдущей строки, расположенных над ним. Это позволяет строить треугольник Паскаля пошагово, используя предыдущую строку.

1) Шестая строка треугольника Паскаля соответствует $n = 6$. Элементы вычисляются как:
$C_6^0 = 1$, так как первый элемент любой строки равен $1$;
$C_6^1 = 6$, получаем из формулы биномиального коэффициента $C_n^m = \frac{n!}{m! (n-m)!} = \frac{6!}{1! \cdot 5!} = 6$;
$C_6^2 = 15$, $C_6^3 = 20$, $C_6^4 = 15$, $C_6^5 = 6$, $C_6^6 = 1$;
Таким образом, шестая строка полностью:
$C_6^0, C_6^1, C_6^2, C_6^3, C_6^4, C_6^5, C_6^6$ или численно $1, 6, 15, 20, 15, 6, 1$.

2) Седьмая строка треугольника Паскаля соответствует $n = 7$. Элементы вычисляются аналогично:
$C_7^0 = 1$, $C_7^1 = 7$, $C_7^2 = 21$, $C_7^3 = 35$, $C_7^4 = 35$, $C_7^5 = 21$, $C_7^6 = 7$, $C_7^7 = 1$;
Таким образом, седьмая строка полностью:
$C_7^0, C_7^1, C_7^2, C_7^3, C_7^4, C_7^5, C_7^6, C_7^7$ или численно $1, 7, 21, 35, 35, 21, 7, 1$.

б) Диагональ треугольных чисел состоит из элементов, которые находятся на наклонной линии, начинающейся с $C_2^0$ и последовательно увеличивающей номера строки и элемента на единицу, но сдвигая элемент на одну позицию вправо в каждой следующей строке. Эти элементы формируют последовательность треугольных чисел:
$C_2^0, C_3^1, C_4^2, C_5^3, C_6^4, C_7^5, C_8^6, C_9^7, \ldots, C_{n+1}^{m-1}$.
Каждый элемент этой диагонали соответствует формуле треугольного числа $T_k = \frac{k(k+1)}{2}$, что демонстрирует связь треугольника Паскаля с последовательностями чисел.

Треугольник Паскаля для наглядности (первые десять строк, нумерация с нуля):