ГДЗ по Алгебре 9 Класс Номер 712 Дорофеев, Суворова — Подробные Ответы

Найдите с помощью треугольника Паскаля $C_5^2$; $C_7^4$; $C_8^6$; $C_9^0$; $C_3^3$.

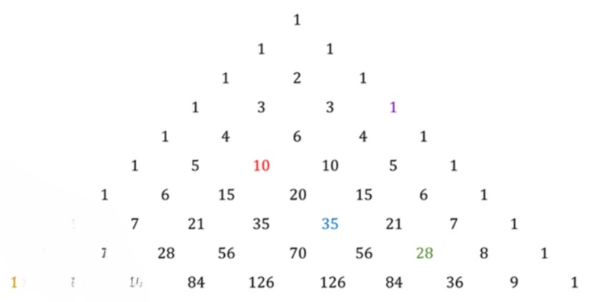
Треугольник Паскаля представлен в задаче 708 (нумерация строк и элементов в строке начинается с нуля):

Значения элементов:
$C_5^2 = 10$;
$C_7^4 = 35$;
$C_8^6 = 28$;
$C_9^0 = 1$;
$C_3^3 = 1$;

Треугольник Паскаля представляет собой треугольную таблицу чисел, в которой каждая строка соответствует номинальному ряду биномиальных коэффициентов, начиная с нулевой строки. Каждое число в строке обозначается как $C_n^k$, где $n$ — номер строки (начиная с 0), а $k$ — порядковый номер элемента в строке (начиная с 0). Значение $C_n^k$ вычисляется как количество сочетаний из $n$ элементов по $k$, то есть $C_n^k = \frac{n!}{k!(n-k)!}$.

Для решения задачи использовался треугольник Паскаля, представленный ниже, где каждая строка содержит элементы, соответствующие биномиальным коэффициентам:

Рассмотрим подробно каждый запрашиваемый биномиальный коэффициент:

1. $C_5^2$ — элемент в 5-й строке (нумерация с нуля) и 2-й позиции (также с нуля). В строке 5: $1, 5, 10, 10, 5, 1$. Элемент с индексом 2 равен $10$. Таким образом, $C_5^2 = 10$.

2. $C_7^4$ — элемент в 7-й строке и 4-й позиции. Строка 7: $1, 7, 21, 35, 35, 21, 7, 1$. Элемент с индексом 4 равен $35$. Следовательно, $C_7^4 = 35$.

3. $C_8^6$ — элемент в 8-й строке и 6-й позиции. Строка 8: $1, 8, 28, 56, 70, 56, 28, 8, 1$. Элемент с индексом 6 равен $28$. Следовательно, $C_8^6 = 28$.

4. $C_9^0$ — элемент в 9-й строке и 0-й позиции. Строка 9: $1, 9, 36, 84, 126, 126, 84, 36, 9, 1$. Элемент с индексом 0 всегда равен $1$. Следовательно, $C_9^0 = 1$.

5. $C_3^3$ — элемент в 3-й строке и 3-й позиции. Строка 3: $1, 3, 3, 1$. Элемент с индексом 3 равен $1$. Следовательно, $C_3^3 = 1$.

Таким образом, используя треугольник Паскаля, каждый биномиальный коэффициент можно определить визуально, без необходимости вычислять факториалы вручную, что значительно упрощает работу с сочетаниями.

Значения элементов:
$C_5^2 = 10$;
$C_7^4 = 35$;
$C_8^6 = 28$;
$C_9^0 = 1$;
$C_3^3 = 1$.