ГДЗ по Алгебре 9 Класс Номер 710 Дорофеев, Суворова — Подробные Ответы

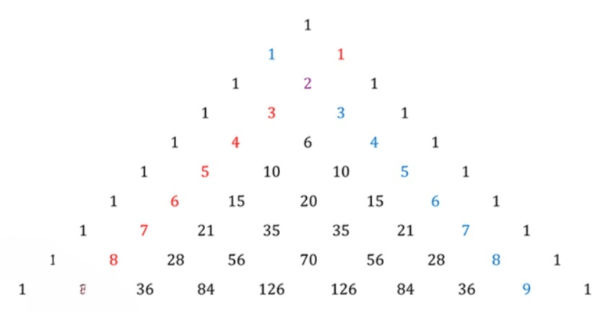
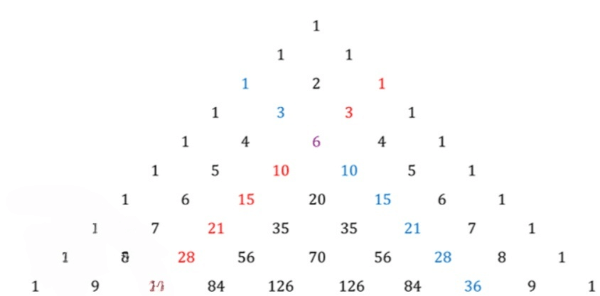
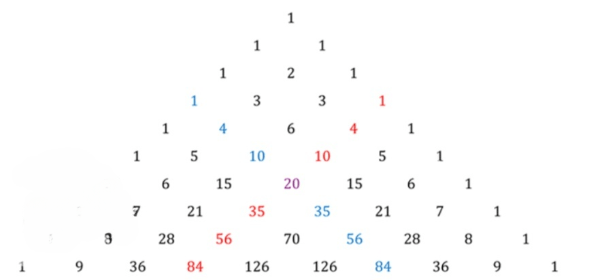
Покажите в треугольнике Паскаля «диагональ», по которой располагается;
а) последовательность натуральных чисел;
б) последовательность треугольных чисел (1; 3; 6; 10; …);
в) последовательность пирамидальных чисел (1; 4; 10; 20; …).

а) Последовательность натуральных чисел:

б) Последовательность треугольных чисел (1; 3; 6; 10; …):

в) Последовательность пирамидальных чисел (1; 4; 10; 20; …):

а) Последовательность натуральных чисел – это последовательность чисел, начинающаяся с единицы, каждое последующее число которой на единицу больше предыдущего. Формально её можно записать как $a_n = n$, где $n$ – номер члена последовательности. Первые десять членов последовательности:

б) Последовательность треугольных чисел формируется суммой первых $n$ натуральных чисел. Каждый член последовательности можно вычислить по формуле $T_n = 1 + 2 + 3 + \cdots + n = \frac{n(n+1)}{2}$, где $n$ – номер члена последовательности. Это объясняется тем, что треугольное число – это количество точек, которые можно расположить в виде равнобедренного треугольника. Первые десять треугольных чисел:
$1, 3, 6, 10, 15, 21, 28, 36, 45, 55$

в) Последовательность пирамидальных чисел формируется суммой первых $n$ треугольных чисел. Каждый член последовательности можно вычислить по формуле $P_n = 1 + 3 + 6 + \cdots + T_n = \frac{n(n+1)(n+2)}{6}$, где $n$ – номер члена последовательности. Пирамидальное число соответствует количеству шаров, которые можно уложить в виде трёхмерной треугольной пирамиды. Первые десять пирамидальных чисел:
$1, 4, 10, 20, 35, 56, 84, 120, 165, 220$