ГДЗ по Алгебре 9 Класс Номер 698 Дорофеев, Суворова — Подробные Ответы

При покупке квартиры в строящемся доме покупатель заключил со строительной фирмой следующий договор: сразу после заключения договора он выплачивает 10% стоимости квартиры, а далее начинает ежемесячно выплачивать 3% от её стоимости. Стоимость купленной им квартиры составляет 600 тыс. р.
а) Составьте формулу для вычисления суммы, выплаченной покупателем квартиры через n месяцев после заключения договора. Вычислите, сколько было выплачено через 1 год; через 2 года после заключения договора.
б) Составьте формулу для вычисления суммы, которую осталось заплатить через n месяцев с начала действия договора, и найдите, сколько останется заплатить через 1 год; через 2 года.
в) На сколько лет рассчитана выплата стоимости квартиры?
г) Проиллюстрируйте графически ситуации, описанные в заданиях «а» и «б», откладывая по горизонтальной оси число лет, в течение которых производится расчёт, а по вертикальной оси — денежные суммы.

а) Имеем арифметическую прогрессию, в которой:
$a_1 = 600 \, 000 \cdot 10\% = 600 \, 000 \cdot 0,1 = 60 \, 000;$
$d = 600 \, 000 \cdot 3\% = 600 \, 000 \cdot 0,03 = 18 \, 000;$
Сумма, которая будет выплачена через $n$ месяцев:
$a_n = a_1 + dn = 60 \, 000 + 18 \, 000n;$
Сумма, которая будет выплачена через 1 год (12 месяцев):
$a_{12} = 60 \, 000 + 18 \, 000 \cdot 12 = 60 \, 000 + 216 \, 000 = 276 \, 000 \, (\text{руб});$
Сумма, которая будет выплачена через 2 года (24 месяца):
$a_{24} = 60 \, 000 + 18 \, 000 \cdot 24 = 60 \, 000 + 432 \, 000 = 492 \, 000 \, (\text{руб});$

б) Имеем арифметическую прогрессию, в которой:
$a_1 = 600 \, 000 — 600 \, 000 \cdot 0,1 = 600 \, 000 — 60 \, 000 = 540 \, 000;$
$d = -600 \, 000 \cdot 0,3 = -18 \, 000;$
Сумма, которую останется выплатить через $n$ месяцев:
$a_n = a_1 + dn = 540 \, 000 — 18 \, 000n;$
Сумма, которую останется выплатить через 1 год (12 месяцев):
$a_{12} = 540 \, 000 — 18 \, 000 \cdot 12 = 540 \, 000 — 216 \, 000 = 324 \, 000 \, (\text{руб});$
Сумма, которую останется выплатить через 2 года (24 месяца):
$a_{24} = 540 \, 000 — 18 \, 000 \cdot 24 = 540 \, 000 — 432 \, 000 = 108 \, 000 \, (\text{руб});$

в) Количество времени, через которое кредит будет выплачен:
$60 \, 000 + 18 \, 000n = 600 \, 000;$
$18 \, 000n = 540 \, 000;$
$n = 30 \, \text{мес} = 2,5 \, \text{года};$

г) Графики данных последовательностей:

а) Имеем арифметическую прогрессию, в которой первый член $a_1$ определяется как 10% от суммы кредита 600 000:
$a_1 = 600 \, 000 \cdot 10\% = 600 \, 000 \cdot 0,1 = 60 \, 000;$
Разность прогрессии $d$ соответствует ежемесячному увеличению на 3% от суммы кредита:
$d = 600 \, 000 \cdot 3\% = 600 \, 000 \cdot 0,03 = 18 \, 000;$
Общая формула суммы выплаты через $n$ месяцев:
$a_n = a_1 + dn = 60 \, 000 + 18 \, 000n;$
Для первого года (12 месяцев) подставляем $n = 12$:
$a_{12} = 60 \, 000 + 18 \, 000 \cdot 12 = 60 \, 000 + 216 \, 000 = 276 \, 000 \, (\text{руб});$
Для второго года (24 месяца) подставляем $n = 24$:
$a_{24} = 60 \, 000 + 18 \, 000 \cdot 24 = 60 \, 000 + 432 \, 000 = 492 \, 000 \, (\text{руб});$

б) Имеем арифметическую прогрессию для остатка долга, в которой первый член $a_1$ равен сумме кредита за вычетом первоначального взноса 10%:
$a_1 = 600 \, 000 — 600 \, 000 \cdot 0,1 = 600 \, 000 — 60 \, 000 = 540 \, 000;$
Разность прогрессии $d$ отрицательная, так как долг уменьшается на 3% от суммы кредита ежемесячно:
$d = -600 \, 000 \cdot 0,03 = -18 \, 000;$
Формула остатка долга через $n$ месяцев:
$a_n = a_1 + dn = 540 \, 000 — 18 \, 000n;$
Через 1 год (12 месяцев):
$a_{12} = 540 \, 000 — 18 \, 000 \cdot 12 = 540 \, 000 — 216 \, 000 = 324 \, 000 \, (\text{руб});$
Через 2 года (24 месяца):
$a_{24} = 540 \, 000 — 18 \, 000 \cdot 24 = 540 \, 000 — 432 \, 000 = 108 \, 000 \, (\text{руб});$

в) Чтобы определить количество месяцев, через которое кредит будет полностью выплачен, приравниваем выплату к полной сумме кредита:
$60 \, 000 + 18 \, 000n = 600 \, 000;$
Вычитаем 60 000 из обеих частей:
$18 \, 000n = 540 \, 000;$
Делим на 18 000:
$n = 30 \, \text{мес} = 2,5 \, \text{года};$

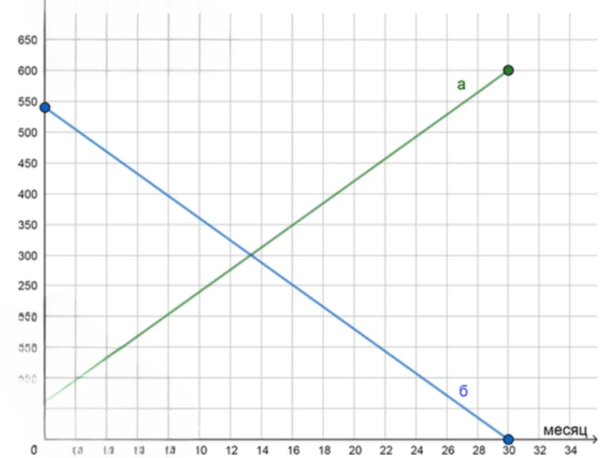
г) Графики данных последовательностей:
График суммы выплат $a_n = 60 \, 000 + 18 \, 000n$ представляет собой возрастающую прямую с началом в 60 000 и углом наклона 18 000 за каждый месяц.
График остатка долга $a_n = 540 \, 000 — 18 \, 000n$ представляет собой убывающую прямую с началом в 540 000 и углом наклона −18 000 за каждый месяц.