ГДЗ по Алгебре 9 Класс Номер 651 Дорофеев, Суворова — Подробные Ответы

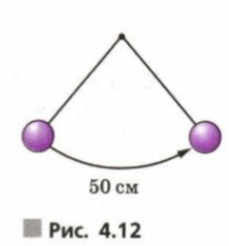
Маятник, раскачиваясь, прошёл сначала расстояние, равное 50 см (рис. 4.12), а затем в каждое следующее движение — расстояние, составляющее 80% от предыдущего. Рассмотрите последовательность, составленную из расстояний, которые проходил маятник за каждое качание.
а) Объясните, почему эта последовательность является геометрической прогрессией, и выпишите её первые пять членов.
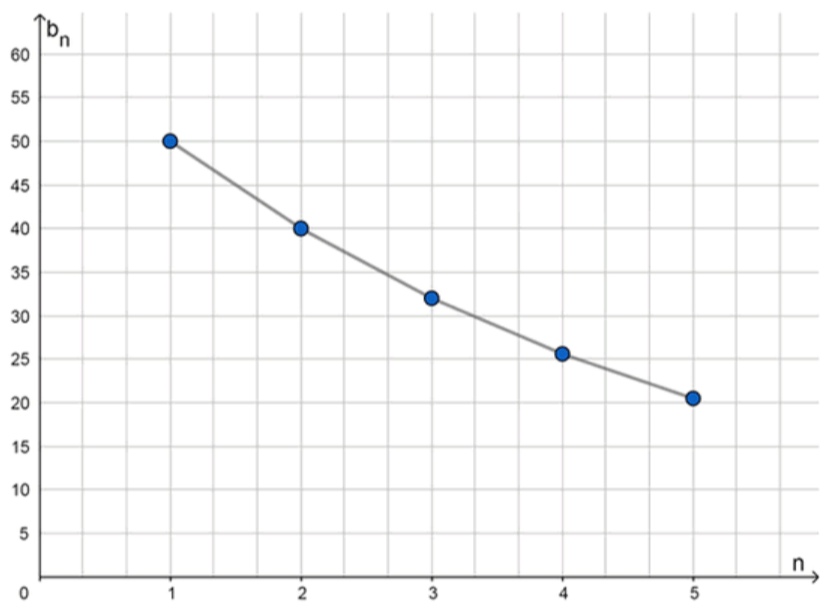
б) Отметьте найденные члены прогрессии точками на координатной плоскости.
в) Запишите формулу n-го члена для этой прогрессии.

а) Последовательность расстояний является геометрической прогрессией, так как каждый её член начиная со второго равен предыдущему члену, умноженному на одно и то же число $0.8$:

$b_1 = 50$ и $q = 0.8$;

$b_2 = b_1 \cdot q = 50 \cdot 0.8 = 40$;

$b_3 = b_2 \cdot q = 40 \cdot 0.8 = 32$;

$b_4 = b_3 \cdot q = 32 \cdot 0.8 = 25.6$;

$b_5 = b_4 \cdot q = 25.6 \cdot 0.8 = 20.48$;

Ответ: $50; 40; 32; 25.6; 20.48; \ldots$.

б) График последовательности:

в) Формула $n$-го члена прогрессии:

$$a_n=a_1\cdot q^{n-1};$$

$$a_n = a_1 \cdot q^{n-1};$$ $$a_n = 50 \cdot 0.8^{n-1};$$

а) Последовательность расстояний является геометрической прогрессией, так как каждый её член начиная со второго равен предыдущему члену, умноженному на одно и то же число $0.8$.

Пусть $b_1 = 50$ и $q = 0.8$ — это первый член прогрессии и коэффициент прогрессии, соответственно.

Чтобы найти второй член прогрессии $b_2$, используем формулу для геометрической прогрессии:

$$b_2 = b_1 \cdot q.$$

Подставляем значения $b_1 = 50$ и $q = 0.8$:

$$b_2 = 50 \cdot 0.8 = 40.$$

Таким образом, второй член прогрессии $b_2 = 40$.

Для нахождения третьего члена прогрессии $b_3$, используем ту же формулу:

$$b_3 = b_2 \cdot q.$$

Подставляем значение $b_2 = 40$ и $q = 0.8$:

$$b_3 = 40 \cdot 0.8 = 32.$$

Таким образом, третий член прогрессии $b_3 = 32$.

Для нахождения четвертого члена прогрессии $b_4$, снова используем формулу:

$$b_4 = b_3 \cdot q.$$

Подставляем значение $b_3 = 32$ и $q = 0.8$:

$$b_4 = 32 \cdot 0.8 = 25.6.$$

Таким образом, четвертый член прогрессии $b_4 = 25.6$.

Для нахождения пятого члена прогрессии $b_5$, применяем ту же формулу:

$$b_5 = b_4 \cdot q.$$

Подставляем значение $b_4 = 25.6$ и $q = 0.8$:

$$b_5 = 25.6 \cdot 0.8 = 20.48.$$

Таким образом, пятый член прогрессии $b_5 = 20.48$.

Ответ: $50; 40; 32; 25.6; 20.48; \ldots$.

б) График последовательности будет показывать экспоненциальное убывание значений, так как каждый следующий член меньше предыдущего, а коэффициент прогрессии $q = 0.8$ меньше 1.

в) Формула $n$-го члена прогрессии:

$$a_n = a_1 \cdot q^{n-1}.$$

Таким образом, для данной прогрессии:

$$a_n = 50 \cdot 0.8^{n-1}.$$