ГДЗ по Алгебре 9 Класс Номер 600 Дорофеев, Суворова — Подробные Ответы

В школе-новостройке сейчас учатся 200 учеников. Допустим, что каждый год число учащихся будет увеличиваться на 20 человек.

а) Запишите формулу для вычисления числа учащихся в школе через $n$ лет.

б) Сколько учащихся будет в школе через 5 лет, если тенденция сохранится?

в) Школа рассчитана на обучение 340 учащихся. Через сколько лет будет достигнута норма?

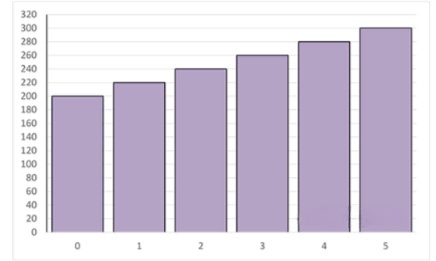
г) Закончите построение столбчатой диаграммы, показав на ней прирост числа учащихся в течение следующих пяти лет (рис. 4.6).

а) $a_1 = 200$ и $d = 20$:

$a_n = a_1 + dn = 200 + 20n;$

б) Количество учащихся через пять лет:

$a_5 = 200 + 20 \cdot 5 = 200 + 100 = 300;$

в) Будет достигнута норма (300 учащихся):

$200 + 20n = 340;$
$20n = 340 — 200;$
$20n = 140, \text{ отсюда } n = 7;$
Ответ: через 7 лет.

г) Прирост учащихся в течение пяти лет:

$a_2 = 200 + 20 \cdot 2 = 200 + 40 = 240;$
$a_3 = 200 + 20 \cdot 3 = 200 + 60 = 260;$
$a_4 = 200 + 20 \cdot 4 = 200 + 80 = 280;$

а) $a_1 = 200$ и $d = 20$:

В данном случае, чтобы записать формулу для $n$-го члена арифметической прогрессии, используем стандартную формулу для арифметической прогрессии:

$$a_n = a_1 + d(n — 1)$$

Подставляем значения первого члена прогрессии $a_1 = 200$ и разности $d = 20$:

$$a_n = 200 + 20(n — 1)$$

Это даёт нам формулу для вычисления $n$-го члена прогрессии.

б) Количество учащихся через пять лет:

Чтобы найти количество учащихся через 5 лет, подставляем $n = 5$ в формулу для $a_n$:

$$a_5 = 200 + 20 \cdot (5 — 1) = 200 + 20 \cdot 4 = 200 + 80 = 300$$

Таким образом, через 5 лет количество учащихся в школе составит $300$ человек.

в) Будет достигнута норма (300 учащихся):

Для того чтобы узнать, через сколько лет количество учащихся в школе станет равно $340$, подставляем $a_n = 340$ в формулу для $n$-го члена прогрессии и решаем относительно $n$:

$$a_n = a_1 + d(n — 1)$$

Подставляем известные значения $a_n = 340$, $a_1 = 200$, $d = 20$:

$$340 = 200 + 20(n — 1)$$

Из этого уравнения решаем для $n$:

$$340-200=20(n-1)$$

$$340 — 200 = 20(n — 1)$$ $$140=20(n-1)$$

$$140 = 20(n — 1)$$ $$n-1=\frac{140}{20}=7$$

$$n — 1 = \frac{140}{20} = 7$$ $$n = 7 + 1 = 8$$

Ответ: через 8 лет.

г) Прирост учащихся в течение пяти лет:

Для того чтобы найти прирост учащихся на каждой из первых пяти минут, подставляем значения $n = 2, 3, 4, 5$ в формулу для $a_n$.

Для $a_2$:

$$a_2 = 200 + 20(2 — 1) = 200 + 20 = 220$$

Для $a_3$:

$$a_3 = 200 + 20(3 — 1) = 200 + 40 = 240$$

Для $a_4$:

$$a_4 = 200 + 20(4 — 1) = 200 + 60 = 260$$

Для $a_5$:

$$a_5 = 200 + 20(5 — 1) = 200 + 80 = 280$$

Для $a_6$:

$$a_6 = 200 + 20(6 — 1) = 200 + 100 = 300$$

Ответ: прирост учащихся в течение пяти лет: $220, 240, 260, 280, 300$.