ГДЗ по Алгебре 9 Класс Номер 599 Дорофеев, Суворова — Подробные Ответы

Самолёт начал снижение на высоте $8000 \, \text{м}$ и в первые десять минут снижался на $500 \, \text{м}$ в минуту.

а) Запишите формулу для вычисления высоты $h_n$, на которой будет находиться самолёт через $n$ минут после начала снижения.

б) С помощью этой формулы определите, на какой высоте будет самолёт через 3 мин после начала снижения; через 8 мин.

в) На какой минуте самолёт окажется ниже $4000 \, \text{м}$ над уровнем земли?

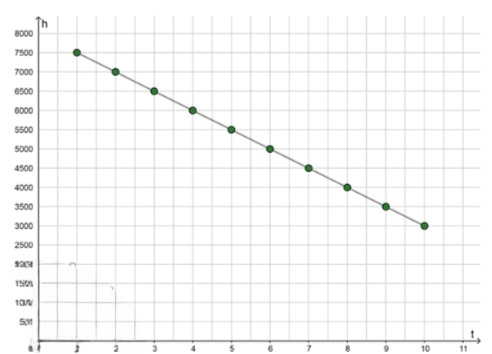
г) Изобразите точками координатной плоскости десять членов последовательности $(h_n)$.

а) $h_1 = 8000$ и $d = -500$:

$h_n = h_1 + dn = 8000 — 500n;$

б) Высота, на которой будет находиться самолёт:

$h_3 = 8000 — 500 \cdot 3 = 8000 — 1500 = 6500 \, (\text{м});$
$h_8 = 8000 — 500 \cdot 8 = 8000 — 4000 = 4000 \, (\text{м});$

в) Самолёт окажется ниже $4000 \, \text{м}$ над уровнем земли в начале девятой минуты, так как через 8 минут он был на высоте $4000 \, \text{м}$;

г) Первые десять членов арифметической прогрессии:

$h_2 = 8000 — 500 \cdot 2 = 8000 — 1000 = 7000 \, (\text{м});$
$h_4 = 8000 — 500 \cdot 4 = 8000 — 2000 = 6000 \, (\text{м});$
$h_5 = 8000 — 500 \cdot 5 = 8000 — 2500 = 5500 \, (\text{м});$
$h_6 = 8000 — 500 \cdot 6 = 8000 — 3000 = 5000 \, (\text{м});$
$h_7 = 8000 — 500 \cdot 7 = 8000 — 3500 = 4500 \, (\text{м});$
$h_9 = 8000 — 500 \cdot 9 = 8000 — 4500 = 3500 \, (\text{м});$
$h_{10} = 8000 — 500 \cdot 10 = 8000 — 5000 = 3000 \, (\text{м});$

а) $h_1 = 8000$ и $d = -500$:

Дана арифметическая прогрессия с первым членом $h_1 = 8000$ и разностью $d = -500$.

Для вычисления $n$-го члена арифметической прогрессии используем формулу общего члена прогрессии:

$$h_n = h_1 + d(n — 1)$$

Где $h_1 = 8000$ — первый член прогрессии, $d = -500$ — разность прогрессии, $n$ — номер члена прогрессии.
3. Подставив эти значения, получаем:

$$h_n = 8000 — 500(n — 1)$$

Эта формула позволяет вычислить высоту на $n$-й минуте после начала снижения самолёта.

б) Высота, на которой будет находиться самолёт:

Для нахождения высоты через 3 минуты подставим $n = 3$ в формулу:

$$h_3 = 8000 — 500(3 — 1) = 8000 — 500 \cdot 2 = 8000 — 1000 = 7000$$

То есть, через 3 минуты высота самолёта будет $h_3 = 7000$ метров.

Для нахождения высоты через 8 минут подставим $n = 8$ в формулу:

$$h_8 = 8000 — 500(8 — 1) = 8000 — 500 \cdot 7 = 8000 — 3500 = 4500$$

То есть, через 8 минут высота самолёта будет $h_8 = 4500$ метров.

в) На какой минуте самолёт окажется ниже $4000 \, \text{м}$ над уровнем земли?

Для нахождения того, когда высота станет меньше 4000 м, подставим $h_n = 4000$ в формулу:

$$4000 = 8000 — 500(n — 1)$$

Решаем это уравнение относительно $n$:

$$4000-8000=-500(n-1)$$

$$4000 — 8000 = -500(n — 1)$$ $$-4000=-500(n-1)$$

$$-4000 = -500(n — 1)$$ $$n-1=\frac{4000}{500}=8$$

$$n — 1 = \frac{4000}{500} = 8$$ $$n = 9$$

Значит, самолёт окажется ниже $4000 \, \text{м}$ на 9-й минуте.

г) Первые десять членов арифметической прогрессии:

Для вычисления первых десяти членов прогрессии будем подставлять значения $n = 1, 2, 3, \dots, 10$ в формулу $h_n = 8000 — 500(n — 1)$.

Для $n = 1$:

$$h_1 = 8000 — 500(1 — 1) = 8000 = 8000 \, \text{м}$$

Для $n = 2$:

$$h_2 = 8000 — 500(2 — 1) = 8000 — 500 = 7500 \, \text{м}$$

Для $n = 3$:

$$h_3 = 8000 — 500(3 — 1) = 8000 — 1000 = 7000 \, \text{м}$$

Для $n = 4$:

$$h_4 = 8000 — 500(4 — 1) = 8000 — 1500 = 6500 \, \text{м}$$

Для $n = 5$:

$$h_5 = 8000 — 500(5 — 1) = 8000 — 2000 = 6000 \, \text{м}$$

Для $n = 6$:

$$h_6 = 8000 — 500(6 — 1) = 8000 — 2500 = 5500 \, \text{м}$$

Для $n = 7$:

$$h_7 = 8000 — 500(7 — 1) = 8000 — 3000 = 5000 \, \text{м}$$

Для $n = 8$:

$$h_8 = 8000 — 500(8 — 1) = 8000 — 3500 = 4500 \, \text{м}$$

Для $n = 9$:

$$h_9 = 8000 — 500(9 — 1) = 8000 — 4000 = 4000 \, \text{м}$$

Для $n = 10$:

$$h_{10} = 8000 — 500(10 — 1) = 8000 — 4500 = 3500 \, \text{м}$$

Ответ: первые десять членов прогрессии: $8000, 7500, 7000, 6500, 6000, 5500, 5000, 4500, 4000, 3500$.