ГДЗ по Алгебре 9 Класс Номер 598 Дорофеев, Суворова — Подробные Ответы

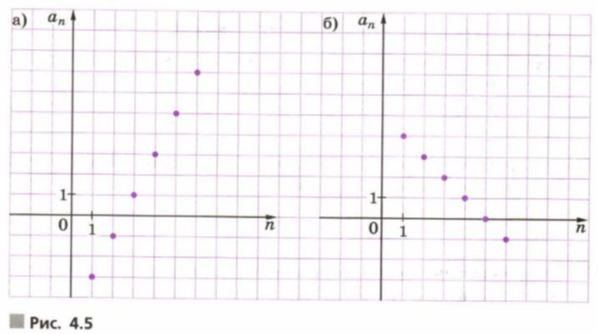
Первые шесть членов арифметической прогрессии $(a_n)$ изображены точками на координатной плоскости (рис. 4.5, $a$, $b$).

Найдите $a_1$ и $d$.

Определим первые шесть членов прогрессии по рисунку:

а) $-3; -1; 1; 3; 5; 7; \dots$:

$a_1 = -3;$
$d = -1 — (-3) = -1 + 3 = 2;$
Ответ: $a_1 = -3$ и $d = 2$.

б) $4; 3; 2; 1; 0; -1; \dots$:

$a_1 = 4;$
$d = 3 — 4 = -1;$
Ответ: $a_1 = 4$ и $d = -1$.

а) $-3; -1; 1; 3; 5; 7; \dots$:

Из данного набора чисел $-3, -1, 1, 3, 5, 7, \dots$ мы видим, что первый член прогрессии $a_1 = -3$.

Разность прогрессии $d$ вычисляется как разница между двумя соседними членами прогрессии. Для этого вычитаем второй член прогрессии из первого:

$$d = -1 — (-3) = -1 + 3 = 2$$

Таким образом, разность прогрессии $d = 2$.

Теперь, имея $a_1 = -3$ и $d = 2$, мы можем записать общую формулу для $n$-го члена арифметической прогрессии:

$$a_n = a_1 + d(n — 1)$$

Где $a_1 = -3$ — первый член прогрессии, а $d = 2$ — разность прогрессии. Это позволяет находить любые члены прогрессии.

Проверим для первых нескольких членов:

• Для $a_1$ имеем:

$$a_1 = -3$$

• Для $a_2$ подставляем $n = 2$:

$$a_2 = -3 + 2(2 — 1) = -3 + 2 = -1$$

• Для $a_3$ подставляем $n = 3$:

$$a_3 = -3 + 2(3 — 1) = -3 + 4 = 1$$

• Для $a_4$ подставляем $n = 4$:

$$a_4 = -3 + 2(4 — 1) = -3 + 6 = 3$$

И так далее. Все члены соответствуют заданной прогрессии.

Ответ: $a_1 = -3$ и $d = 2$.

б) $4; 3; 2; 1; 0; -1; \dots$:

Из данной последовательности $4, 3, 2, 1, 0, -1, \dots$ видим, что первый член прогрессии $a_1 = 4$.

Для нахождения разности прогрессии $d$, вычитаем второй член из первого:

$$d = 3 — 4 = -1$$

Таким образом, разность прогрессии $d = -1$.

Теперь, имея $a_1 = 4$ и $d = -1$, мы можем записать формулу для общего члена прогрессии:

$$a_n = a_1 + d(n — 1)$$

Где $a_1 = 4$ — первый член прогрессии, а $d = -1$ — разность прогрессии.

Проверим для первых нескольких членов:

• Для $a_1$ имеем:

$$a_1 = 4$$

• Для $a_2$ подставляем $n = 2$:

$$a_2 = 4 + (-1)(2 — 1) = 4 — 1 = 3$$

• Для $a_3$ подставляем $n = 3$:

$$a_3 = 4 + (-1)(3 — 1) = 4 — 2 = 2$$

• Для $a_4$ подставляем $n = 4$:

$$a_4 = 4 + (-1)(4 — 1) = 4 — 3 = 1$$

И так далее. Все члены соответствуют заданной прогрессии.

Ответ: $a_1 = 4$ и $d = -1$.