ГДЗ по Алгебре 9 Класс Номер 571 Дорофеев, Суворова — Подробные Ответы

Предположим, что родители дали вам 1 рубль и у вас имеются две возможности дальнейшего получения денег. Первая: ежедневно вы будете получать сумму, на 2 рубля большую, чем получили в предыдущий день. Вторая: во второй день вы получите 1 рубль, а начиная с третьего дня будете получать ежедневно столько рублей, сколько получили за предшествующие два дня вместе.
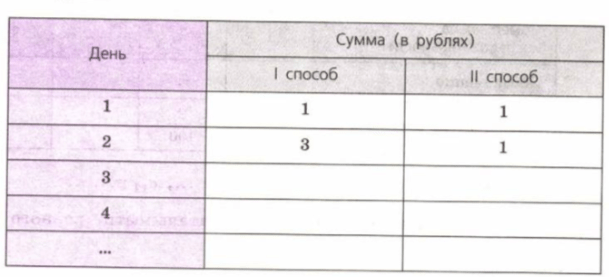
1) Заполните таблицу для первых десяти дней.

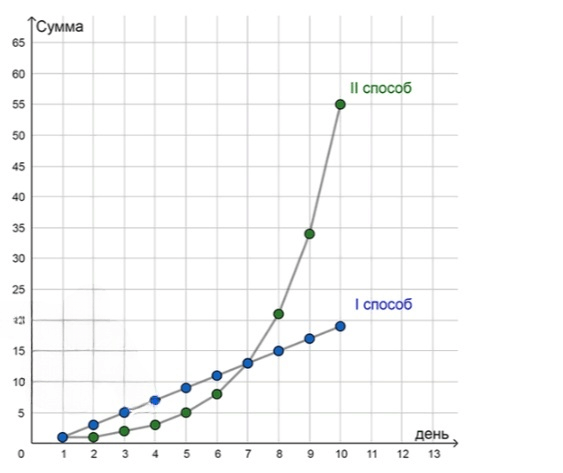
2) Изобразите каждую из получившихся последовательностей точками на координатной плоскости: по горизонтальной оси откладывайте номер дня, а по вертикальной — полученную в этот день сумму денег. Какой из способов выгоднее, если вы планируете получать деньги в течение одной недели? в течение одного месяца?
3) Задайте каждую из этих последовательностей рекуррентным способом, обозначив первую из них через (a_n), а вторую — через (b_n).

1) Таблица суммы денег для первых десяти дней:

$$\begin{array}{|c|c|c|} \hline \text{День} & \multicolumn{2}{c|}{\text{Сумма (в рублях)}} \\ \hline & I \text{ способ} & II \text{ способ} \\ \hline 1 & 1 & 1 \\ \hline 2 & 3 & 1 \\ \hline 3 & 5 & 2 \\ \hline 4 & 7 & 3 \\ \hline 5 & 9 & 5 \\ \hline 6 & 11 & 8 \\ \hline 7 & 13 & 13 \\ \hline 8 & 15 & 21 \\ \hline 9 & 17 & 34 \\ \hline 10 & 19 & 55 \\ \hline \end{array}$$

2) Графики данных последовательностей:

В течение одной недели выгоднее получать деньги первым способом;
В течение одного месяца выгоднее получать деньги вторым способом;

3) Зададим каждую последовательность:
$a_1 = 1$, $a_n = a_{n-1} + 2$, где $n \geq 2$;
$b_1 = 1$, $b_2 = 1$, $b_n = b_{n-1} + b_{n-2}$, где $n \geq 3$;

1) Таблица суммы денег для первых десяти дней:

$$\begin{array}{|c|c|c|} \hline \text{День} & \multicolumn{2}{c|}{\text{Сумма (в рублях)}} \\ \hline & I \text{ способ} & II \text{ способ} \\ \hline 1 & 1 & 1 \\ \hline 2 & 3 & 1 \\ \hline 3 & 5 & 2 \\ \hline 4 & 7 & 3 \\ \hline 5 & 9 & 5 \\ \hline 6 & 11 & 8 \\ \hline 7 & 13 & 13 \\ \hline 8 & 15 & 21 \\ \hline 9 & 17 & 34 \\ \hline 10 & 19 & 55 \\ \hline \end{array}$$

2) Графики данных последовательностей:

В течение одной недели выгоднее получать деньги первым способом;
В течение одного месяца выгоднее получать деньги вторым способом;

3) Зададим каждую последовательность:

Последовательность $a_n$:

Начальное значение $a_1 = 1$, для всех $n \geq 2$ выполняется рекуррентное соотношение:

$$a_n = a_{n-1} + 2$$

Это линейная последовательность с разностью между каждым соседним элементом, равной 2. То есть каждый элемент последовательности $a_n$ можно получить, начиная с первого, прибавляя 2 к предыдущему значению.

Пример вычисления первых значений:

$$a_1 = 1$$ $$a_2 = a_1 + 2 = 1 + 2 = 3$$ $$a_3 = a_2 + 2 = 3 + 2 = 5$$ $$a_4 = a_3 + 2 = 5 + 2 = 7$$

Таким образом, последовательность $a_n$ имеет вид:

$$a_1 = 1, a_2 = 3, a_3 = 5, a_4 = 7, a_5 = 9, \dots$$

Последовательность $b_{}$$b_n$:

Начальные значения $b_1 = 1$ и $b_2 = 1$, для всех $n \geq 3$ выполняется рекуррентное соотношение:

$$b_n = b_{n-1} + b_{n-2}$$

Это последовательность, построенная по принципу фибоначчи. Каждый следующий элемент последовательности $b_n$ является суммой двух предыдущих. Для первых элементов последовательности:

$$b_1 = 1, b_2 = 1$$ $$b_3 = b_2 + b_1 = 1 + 1 = 2$$ $$b_4 = b_3 + b_2 = 2 + 1 = 3$$ $$b_5 = b_4 + b_3 = 3 + 2 = 5$$ $$b_6 = b_5 + b_4 = 5 + 3 = 8$$

Таким образом, последовательность $b_n$ имеет вид:

$$b_1 = 1, b_2 = 1, b_3 = 2, b_4 = 3, b_5 = 5, b_6 = 8, \dots$$