ГДЗ по Алгебре 9 Класс Номер 559 Дорофеев, Суворова — Подробные Ответы

На рисунке 3.28 изображены графики уравнений $(y-0,5x^2)(y-2)=0$ и $\frac{y-0,5x^2}{y-2}=0$. График первого уравнения состоит из параболы $y=0,5x^2$ и прямой $y=2$, т. е. он является их объединением. График второго уравнения — это парабола $y=0,5x^2$ без точек, принадлежащих прямой $y=2$.

Рассуждая аналогично, постройте графики уравнений:

а) $(x^2+y^2-4)(y^2-x^2)=0,\frac{x^2+y^2-4}{y^2-x^2}=0,\frac{y^2-x^2}{x^2+y^2-4}=0;$

б) $(xy-2)(y-2x)=0,\frac{xy-2}{y-2x}=0,\frac{y-2x}{xy-2}=0.$

а) $(x^2+y^2-4)(y^2-x^2)=0;$

${\mathrm{1)\; y}}^2-x^2=0;$

$y^2=x^2,$ отсюда $\mathrm{\mid }y\mathrm{\mid }=\mathrm{\mid }x\mathrm{\mid }:$

${\mathrm{2)\; x}}^2+y^2-4=0;$

$x^2+y^2=4\text{— уравнение окружности:}$

$x_0=0$ и $y_0=0,$ $R=\sqrt{4}=2;$

$(x^2+y^2-4)(y^2-x^2)=0:$

$\frac{x^2+y^2-4}{y^2-x^2}=0:$

$\frac{x^2 + y^2 — 4}{y^2 — x^2} = 0: y2−x2x2+y2−4=0:$$\frac{y^2 — x^2}{x^2 + y^2 — 4} = 0:$

б) $(xy-2)(y-2x)=0;$

$\mathrm{1)\; x}y-2=0,$ отсюда $y=\frac{2}{x}\text{— уравнение гиперболы:}$

$\mathrm{2)\; y}-2x=0,$ отсюда $y=2x\text{— уравнение прямой:}$

$(xy-2)(y-2x)=0:$

$(xy — 2)(y — 2x) = 0:$

$\frac{xy-2}{y-2x}=0:$

$\frac{xy — 2}{y — 2x} = 0:$

$\frac{y-2x}{xy-2}=0:$

$$\frac{y — 2x}{xy — 2} = 0:

а) $(x^2+y^2-4)(y^2-x^2)=0;$$$

1) Разделим уравнение на два случая. Первый случай — $y^2-x^2=0$, что можно записать как:

$$y^2=x^2\Rightarrow \mathrm{\mid }y\mathrm{\mid }=\mathrm{\mid }x\mathrm{\mid }\mathrm{.}$$

Это означает, что $y$ либо равно $x$, либо равно $-x$. Теперь подставим различные значения $x$ и находим соответствующие значения $y$:

• Когда $x=-1$, то $y_1=-1$, и $y_2=1$.
• Когда $x=0$, то $y_1=0$, и $y_2=0$.
• Когда $x=1$, то $y_1=-1$, и $y_2=1$.

Таким образом, получаем два множества решений для $y$, $y_1=-x$ и $y_2=x$.

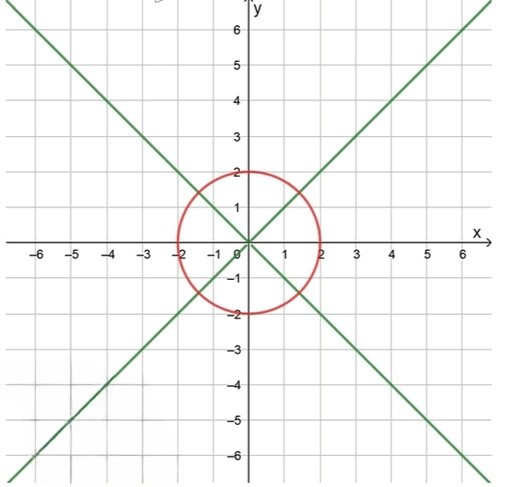
2) Рассмотрим второй случай $x^2+y^2-4=0$. Это уравнение представляет собой уравнение окружности с центром в точке $(0,0)$ и радиусом $2$:

$$x^2+y^2=4.$$

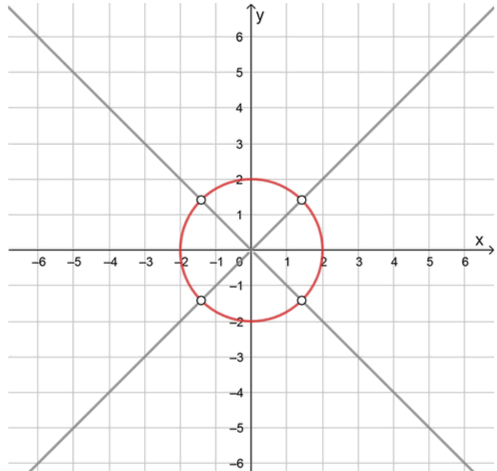
Теперь, чтобы найти графическую иллюстрацию, отметим, что окружность пересекает оси координат в точках $(2,0)$, $(-2,0)$, $(0,2)$ и $(0,-2)$.

3) Теперь рассмотрим весь график. Первое уравнение $(x^2+y^2-4)(y^2-x^2)=0$ говорит, что либо у нас окружность, либо гипербола. Второе уравнение $\frac{x^2+y^2-4}{y^2-x^2}=0$ может быть преобразовано в:

$$x^2+y^2-4=0.$$

График этого уравнения — это окружность радиусом 2 с центром в начале координат. Третье уравнение $\frac{y^2-x^2}{x^2+y^2-4}=0$ также приводит к уравнению гиперболы.

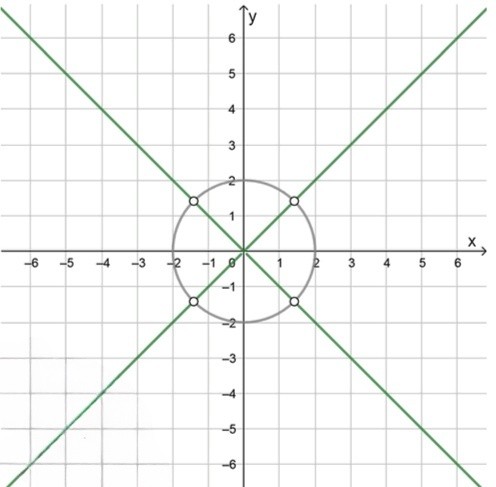
Ответ: Для уравнений $(x^2+y^2-4)(y^2-x^2)=0$, график состоит из окружности и гиперболы, а для $\frac{x^2+y^2-4}{y^2-x^2}=0$, график — это окружность.

б) $(xy-2)(y-2x)=0;$

1) Разделим уравнение на два случая. Первый случай — $xy-2=0$, отсюда:

$$xy=2\Rightarrow y=\frac{2}{x}\mathrm{.}$$

Это уравнение представляет гиперболу, поскольку оно имеет вид $y=\frac{2}{x}$. Рассмотрим, как оно изменяется при разных значениях $x$:

• Когда $x=-4$, то $y=\frac{2}{-4}=-0.5$.
• Когда $x=-2$, то $y=\frac{2}{-2}=-1$.
• Когда $x=-1$, то $y=\frac{2}{-1}=-2$.
• Когда $x=-0.5$, то $y=\frac{2}{-0.5}=-4$.
• Когда $x=0.5$, то $y=\frac{2}{0.5}=4$.
• Когда $x=1$, то $y=\frac{2}{1}=2$.
• Когда $x=2$, то $y=\frac{2}{2}=1$.
• Когда $x=4$, то $y=\frac{2}{4}=0.5$.

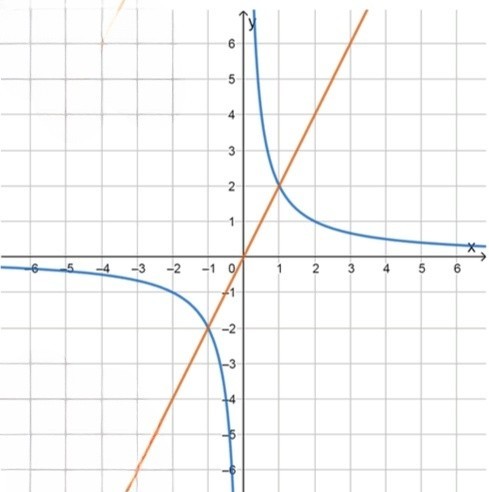
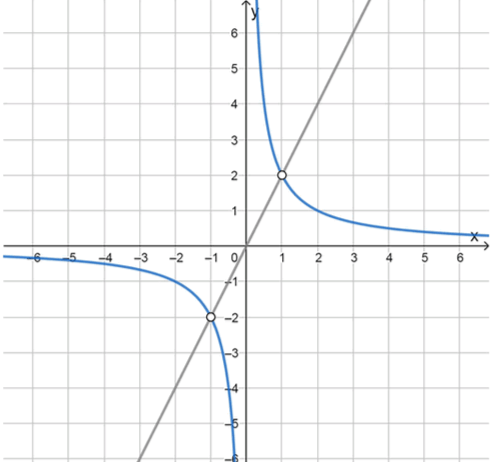
График этого уравнения представляет собой гиперболу, расположенную в первой и третьей четвертях.

2) Рассмотрим второй случай $y-2x=0$, отсюда:

$$y=2x\mathrm{.}$$

Это уравнение прямой с угловым коэффициентом 2. Рассмотрим несколько значений $x$:

• Когда $x=0$, то $y=0$.
• Когда $x=2$, то $y=4$.
• Когда $x=-2$, то $y=-4$.

График этого уравнения — это прямая, проходящая через начало координат с угловым коэффициентом 2.

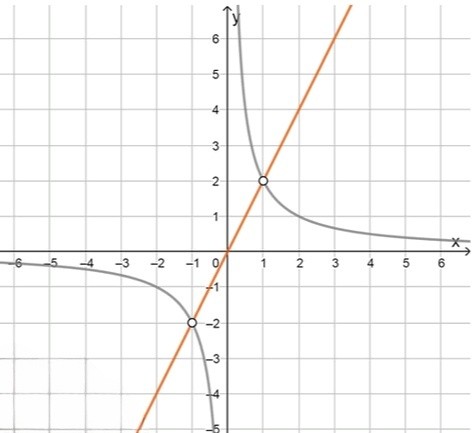
Рассмотрим весь график. Первое уравнение $(xy-2)(y-2x)=0$ представляет собой объединение гиперболы $y=\frac{2}{x}$ и прямой $y=2x$. Второе уравнение $\frac{xy-2}{y-2x}=0$ приводит к уравнению гиперболы, а третье уравнение $\frac{y-2x}{xy-2}=0$ приводит к прямой.

Ответ: Для уравнений $\frac{y-2x}{xy-2}=0:$, график состоит из гиперболы и прямой.