ГДЗ по Алгебре 9 Класс Номер 558 Дорофеев, Суворова — Подробные Ответы

1) Докажите алгебраическим методом, что система уравнений

$\begin{cases} 2x — y = 4 \\ x + y = 2 \\ x^2 + y^2 = 4 \end{cases}$

имеет решение, и притом только одно. Дайте графическую иллюстрацию данного утверждения.

2) Найдите такое значение $r$, при котором система уравнений

$\begin{cases} x — y = -3 \\ x + 2y = 6 \\ x^2 + y^2 = r^2 \end{cases}$

имеет решение.

I)

Доказательство алгебраическим методом:

$\begin{cases} 2x — y = 4 \\ x + y = 2 \\ x^2 + y^2 = 4 \end{cases}$

Решим систему из первых двух уравнений:

$2x — y = 4,$ отсюда $y = 2x — 4;$

$x + 2x — 4 = 2;$

$3x = 2 + 4;$

$3x = 6,$ отсюда $x = 2;$

$y = 2 \cdot 2 — 4 = 4 — 4 = 0;$

Проверим, является ли оно решением третьего уравнения:

$2^2 + 0^2 = 4;$

$4 = 4 \quad \text{— верно;}$

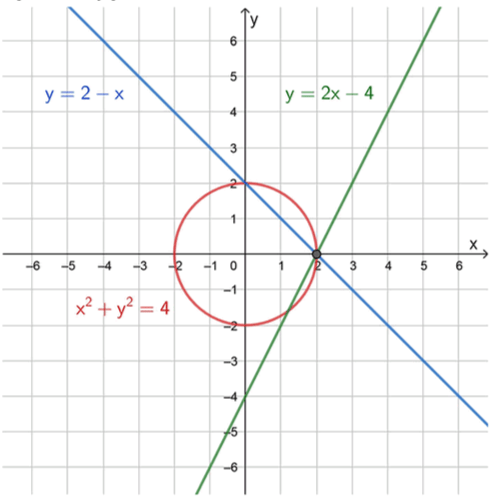
Графическая иллюстрация:

$2x — y = 4 \quad => \quad y = 2x — 4 \quad \text{— уравнение прямой:}$

$x + y = 2 \quad => \quad y = 2 — x \quad \text{— уравнение прямой:}$

$x^2 + y^2 = 4 \quad \text{— уравнение окружности:}$

$x_0 = 0$ и $y_0 = 0,$ $R=\sqrt{4}=2;$

$$Графики всех трех функций пересекаются только в одной точке;

II)

$\begin{cases} x — y = -3 \\ x + 2y = 6 \\ x^2 + y^2 = r^2 \end{cases}$

$x — y = -3,$ отсюда $y = x + 3;$

$x + 2(x + 3) = 6;$

$x + 2x + 6 = 6;$

$3x = 6 — 6;$

$3x = 0,$ отсюда $x = 0;$

$y = 0 + 3 = 3;$

$r^2 = 0^2 + 3^2;$

$r^2 = 9,$ отсюда $r = \pm 3;$

Ответ: $r = \pm 3.$

I)

Доказательство алгебраическим методом:

$\begin{cases} 2x — y = 4 \\ x + y = 2 \\ x^2 + y^2 = 4 \end{cases}$

Из первого уравнения $2x — y = 4$ выразим $y$ через $x$:

$$y = 2x — 4.$$

Подставим $y = 2x — 4$ во второе уравнение $x + y = 2$:

$$x + (2x — 4) = 2.$$

Упростим:

$$3x — 4 = 2.$$

Теперь перенесем -4 в правую часть:

$$3x = 2 + 4 \quad \Rightarrow \quad 3x = 6 \quad \Rightarrow \quad x = \frac{6}{3} = 2.$$

Подставим $x = 2$ в $y = 2x — 4$:

$$y = 2 \cdot 2 — 4 = 4 — 4 = 0.$$

Проверим, является ли найденное решение $x = 2$ и $y = 0$ решением третьего уравнения $x^2 + y^2 = 4$:

$$2^2 + 0^2 = 4 \quad \Rightarrow \quad 4 = 4 \quad \text{— верно.}$$

Графическая иллюстрация:

Уравнение $2x — y = 4$ преобразуется в $y = 2x — 4$, это уравнение прямой. Подставим разные значения $x$ для построения таблицы:

$$\begin{array}{|c|c|} \hline x & y \\ \hline 0 & -4 \\ 2 & 0 \\ \hline \end{array}$$

Уравнение $x + y = 2$ преобразуется в $y = 2 — x$, это также уравнение прямой. Подставим разные значения $x$:

$$\begin{array}{|c|c|} \hline x & y \\ \hline 0 & 2 \\ 2 & 0 \\ \hline \end{array}$$

Уравнение $x^2 + y^2 = 4$ — это уравнение окружности с центром в $(0, 0)$ и радиусом $R = \sqrt{4} = 2$. Подставим значения $x$ и найдем $y$:

$$\begin{array}{|c|c|} \hline x & y \\ \hline 2 & 0 \\ 0 & 2 \\ \hline \end{array}$$

Все три графика пересекаются только в одной точке $(2, 0)$.

Ответ: $(2; 0)$.

II)

$\begin{cases} x — y = -3 \\ x + 2y = 6 \\ x^2 + y^2 = r^2 \end{cases}$

Из первого уравнения $x — y = -3$ выразим $y$ через $x$:

$$y = x + 3.$$

Подставим $y = x + 3$ во второе уравнение $x + 2y = 6$:

$$x + 2(x + 3) = 6.$$

Раскроем скобки:

$$x + 2x + 6 = 6 \quad \Rightarrow \quad 3x + 6 = 6.$$

Теперь перенесем 6 в правую часть:

$$3x = 6 — 6 \quad \Rightarrow \quad 3x = 0 \quad \Rightarrow \quad x = 0.$$

Подставим $x = 0$ в $y = x + 3$:

$$y = 0 + 3 = 3.$$

Подставим $x = 0$ и $y = 3$ в уравнение $x^2 + y^2 = r^2$:

$$0^2 + 3^2 = r^2 \quad \Rightarrow \quad 9 = r^2 \quad \Rightarrow \quad r = \pm 3.$$

Ответ: $r = \pm 3$.