ГДЗ Дорофеев 9 Класс по Алгебре Шарыгин Учебник 📕 Суворова- Все Части

ГДЗ по Алгебре 9 Класс Номер 531 Дорофеев, Суворова - Подробные Ответы

Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. и др.

9 класс

Тип

ГДЗ, Решебник.

Автор

Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. и др.

Год

2022.

Издательство

Просвещение.

Описание

Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.

Оцени решение

← Предыдущий Следующий →

Сообщить об ошибке

ГДЗ по Алгебре 9 Класс Номер 531 Дорофеев, Суворова — Подробные Ответы

Задача

Постройте график функции:

а) $y = \begin{cases} \frac{x^2 — 1}{x — 1}, & \text{если } x > 0 \\ \frac{x^2 — 1}{1 — x}, & \text{если } x \leq 0 \end{cases};$

б) $y = \begin{cases} \frac{x^2 — 4}{x — 2}, & \text{если } x \geq 0 \\ \frac{x^2 — 4}{x + 2}, & \text{если } x < 0 \end{cases}.$

Краткий ответ

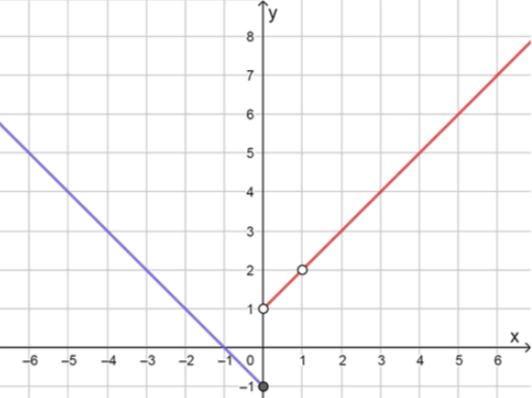
а) $y = \begin{cases} \frac{x^2 — 1}{x — 1}, & \text{если } x > 0 \\ \frac{x^2 — 1}{1 — x}, & \text{если } x \leq 0 \end{cases};$

$y = \frac{x^2 — 1}{x — 1} = \frac{(x — 1)(x + 1)}{x — 1} = x + 1:$

$x — 1 \neq 0,$ отсюда $x \neq 1;$

$x$	$-1$	$0$
$y$	$0$	$1$

$y = \frac{x^2 — 1}{1 — x} = \frac{(x — 1)(x + 1)}{1 — x} = \frac{-(1 — x)(x + 1)}{1 — x} = -x — 1:$

$1 — x \neq 0,$ отсюда $x \neq 1;$

$x$	$-1$	$0$
$y$	$0$	$-1$

б) $y = \begin{cases} \frac{x^2 — 4}{x — 2}, & \text{если } x \geq 0 \\ \frac{x^2 — 4}{x + 2}, & \text{если } x < 0 \end{cases};$

$y = \frac{x^2 — 4}{x — 2} = \frac{(x — 2)(x + 2)}{x — 2} = x + 2:$

$x — 2 \neq 0,$ отсюда $x \neq 2;$

$x$	$-2$	$0$
$y$	$0$	$2$

$y = \frac{x^2 — 4}{x + 2} = \frac{(x — 2)(x + 2)}{x + 2} = x — 2:$

$x + 2 \neq 0,$ отсюда $x \neq -2;$

$x$	$0$	$2$
$y$	$-2$	$0$

Подробный ответ

а) $y = \begin{cases} \frac{x^2 — 1}{x — 1}, & \text{если } x > 0 \\ \frac{x^2 — 1}{1 — x}, & \text{если } x \leq 0 \end{cases};$

1. Рассмотрим первый случай $y = \frac{x^2 — 1}{x — 1}$ . Используем разложение числителя на множители:

$x^2 — 1 = (x — 1)(x + 1)$

Таким образом, функция примет вид:

$y = \frac{(x — 1)(x + 1)}{x — 1}$

При условии, что $x \neq 1$ (так как $x — 1 \neq 0$ ), мы можем сократить $x — 1$ в числителе и знаменателе:

$y = x + 1$

Таким образом, для $x > 0$ функция будет равна:

$y = x + 1$

Теперь подставим несколько значений для $x$ :

$x$	$-1$	$0$
$y$	$0$	$1$

2. Рассмотрим второй случай $y = \frac{x^2 — 1}{1 — x}$ . Мы также можем разложить числитель на множители:

$x^2 — 1 = (x — 1)(x + 1)$

Теперь подставим это в выражение для функции:

$y = \frac{(x — 1)(x + 1)}{1 — x}$

Мы можем заметить, что $1 — x = -(x — 1)$ , и, соответственно, получаем:

$y = \frac{-(x — 1)(x + 1)}{x — 1}$

Сокращаем $x — 1$ в числителе и знаменателе при условии, что $x \neq 1$ :

$y = -(x + 1)$

Таким образом, для $x \leq 0$ функция будет равна:

$y = -x — 1$

Теперь подставим несколько значений для $x$ :

$x$	$-1$	$0$
$y$	$0$	$-1$

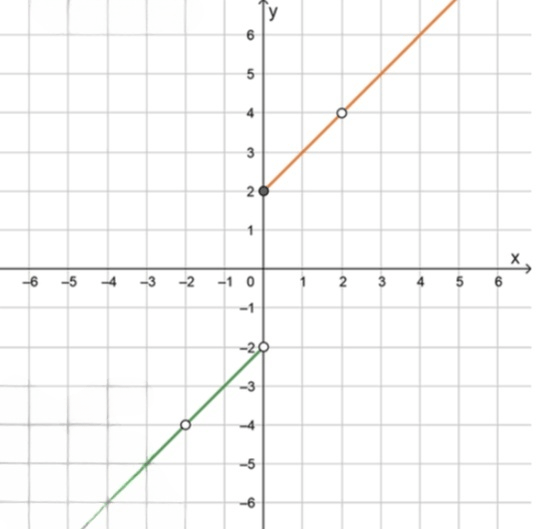
б) $y = \begin{cases} \frac{x^2 — 4}{x — 2}, & \text{если } x \geq 0 \\ \frac{x^2 — 4}{x + 2}, & \text{если } x < 0 \end{cases};$

1. Рассмотрим первый случай $y = \frac{x^2 — 4}{x — 2}$ . Разложим числитель на множители:

$x^2 — 4 = (x — 2)(x + 2)$

Теперь подставим это в выражение для функции:

$y = \frac{(x — 2)(x + 2)}{x — 2}$

При условии, что $x \neq 2$ (так как $x — 2 \neq 0$ ), мы можем сократить $x — 2$ в числителе и знаменателе:

$y = x + 2$

Таким образом, для $x \geq 0$ функция будет равна:

$y = x + 2$

Теперь подставим несколько значений для $x$ :

$x$	$-2$	$0$
$y$	$0$	$2$

2. Рассмотрим второй случай $y = \frac{x^2 — 4}{x + 2}$ . Разложим числитель на множители:

$x^2 — 4 = (x — 2)(x + 2)$

Теперь подставим это в выражение для функции:

$y = \frac{(x — 2)(x + 2)}{x + 2}$

При условии, что $x \neq -2$ (так как $x + 2 \neq 0$ ), мы можем сократить $x + 2$ в числителе и знаменателе:

$y = x — 2$

Таким образом, для $x < 0$ функция будет равна:

$y = x — 2$

Теперь подставим несколько значений для $x$ :

$x$	$0$	$2$
$y$	$-2$	$0$

Оцени решение

← Предыдущий Следующий →

Сообщить об ошибке

Общая оценка

4.4 / 5

Комментарии

Оставь свой отзыв 💬

Комментариев пока нет, будьте первым!

Другие предметы

ГДЗ Дорофеев 7, 8, 9 Класс по Алгебре Все Учебники - Ответы на Любые Задачи Бесплатно

7-9 класс

7 8 9

ГДЗ Дорофеев 1, 2, 3, 4, 5, 6 Класс по Математике Все Учебники - Ответы на Любые Задачи Бесплатно

1-6 класс

1 2 3 4 5 6