ГДЗ по Алгебре 9 Класс Номер 504 Дорофеев, Суворова — Подробные Ответы

Дана система уравнений с переменными $x$ и $y$:

$$\begin{cases} x^2 + y^2 = 1 \\ y = |x| + a \end{cases}$$

а) С помощью графиков установите, сколько решений может иметь система уравнений.
б) Найдите значения $a$, при которых система имеет два решения; три решения.

$$\begin{cases} x^2 + y^2 = 1 \\ y = |x| + a \end{cases}$$

а)

$x^2 + y^2 = 1$ — уравнение окружности:
$x_0 = 0$ и $y_0 = 0$, $R = \sqrt{1} = 1$;

$y = |x| + a$ — уравнение графика модуля:
Вершина находится в точке $(0; a)$;

3) Графики функций:

Система уравнений может иметь: 0 решений, 1 решение, 2 решения, 3 решения, 4 решения;

б)

Система имеет два решения при: $-1 < a < 1$ и $a = -\sqrt{2}$;
Система имеет три решения при $a = -1$.

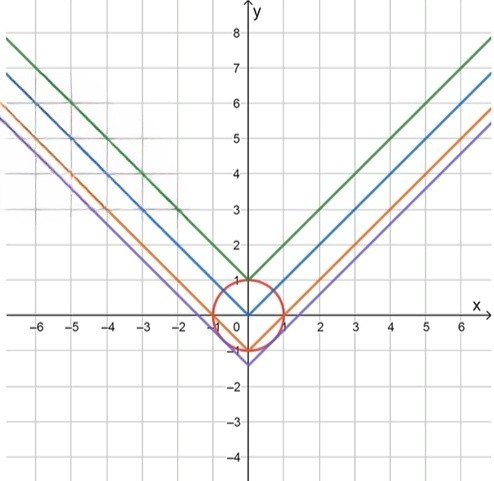
а) Рассмотрим уравнение $x^2 + y^2 = 1$. Это уравнение окружности с центром в точке $(0, 0)$ и радиусом $R = \sqrt{1} = 1$. Данное уравнение описывает окружность с радиусом 1, которая расположена на плоскости $xy$ и пересекает оси $x$ и $y$ в точках $x = \pm 1$ и $y = \pm 1$.

Теперь рассмотрим уравнение $y = |x| + a$. Это уравнение графика модуля. Функция $y = |x| + a$ имеет форму буквы «V», где вершина этой буквы находится в точке $(0, a)$. Функция возрастает как для положительных значений $x$, так и для отрицательных, с угловым коэффициентом $1$ для $x \geq 0$ и угловым коэффициентом $-1$ для $x < 0$.

Для того чтобы определить количество решений системы, нужно рассмотреть, как графики этих двух функций пересекаются. Первая функция — это окружность, вторая — это график функции модуля. В зависимости от значения параметра $a$, количество точек пересечения будет меняться.

Если $a$ слишком велико или слишком мало, график модуля может не пересекаться с окружностью вообще (0 решений).

Если $a$ такое, что график модуля касается окружности в одной точке, то система имеет одно решение.

Если график модуля пересекает окружность в двух точках, то система имеет два решения.

Если график модуля пересекает окружность в четырех точках, то система имеет четыре решения.

Ответ: система уравнений может иметь 0 решений, 1 решение, 2 решения, 3 решения или 4 решения.

б) Рассмотрим, при каких значениях $a$ система имеет два решения. Для того чтобы система имела два решения, график функции $y = |x| + a$ должен пересекать окружность в двух точках. Для этого требуется, чтобы график модуля $y = |x| + a$ находился достаточно близко к окружности, но не пересекал её больше, чем в двух точках.

Для этого нужно, чтобы значение $a$ было в пределах от $-1$ до $1$, то есть при $-1 < a < 1$ система имеет два решения. Также система будет иметь два решения, если $a = -\sqrt{2}$, потому что это значение параметра приводит к тому, что график модуля пересекает окружность в двух точках.

Ответ: система имеет два решения при $-1 < a < 1$ и $a = -\sqrt{2}$.

Рассмотрим, при каких значениях $a$ система имеет три решения. Система будет иметь три решения, если график функции $y = |x| + a$ будет касаться окружности в одной точке и затем пересекать её в другой. Это может происходить только при значении $a = -1$, когда график модуля будет касаться окружности в одной точке, а затем пересекать её в другой.

Ответ: система имеет три решения при $a = -1$.