
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 503 Дорофеев, Суворова — Подробные Ответы
С помощью графиков выясните, сколько корней может иметь уравнение ( — параметр):
а) ;
б) .
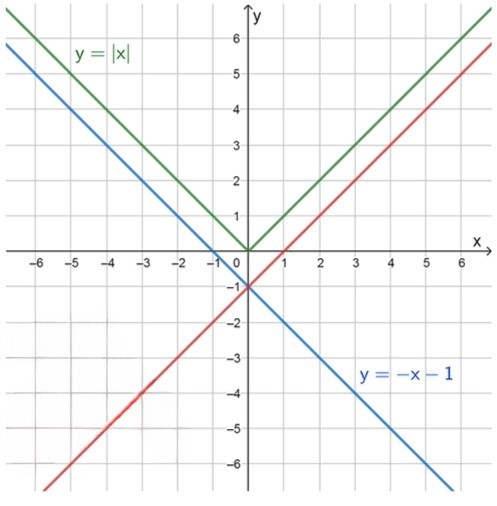
а) :
— уравнение графика модуля:
— уравнение прямой:
График пересекает ось в точке с ординатой ;
При , получим функцию :
При , получим функцию :
3) Построим графики функций:
Ответ: нет корней при ; 1 корень при .
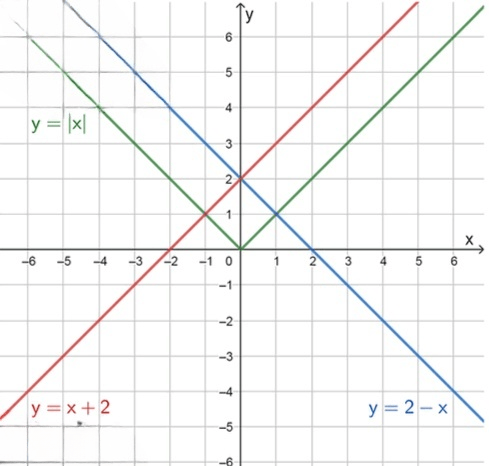
б) :
— уравнение графика модуля:
— уравнение прямой:
График пересекает ось в точке с ординатой ;
При , получим функцию :
При , получим функцию :
3) Построим графики функций:
Ответ: 1 корень при ; 2 корня при .
а) :
Рассмотрим функцию , которая представляет собой график модуля. Модуль функции имеет вид:
Таблица значений для функции :
График этой функции — это угол, образующий две части: одна из них восходящая (при ), а другая — нисходящая (при ).
Теперь рассмотрим прямую . Это линейная функция с угловым коэффициентом и пересечением с осью в точке .
При , получаем функцию , которая пересекает ось в точке и ось в точке . Для некоторых значений эта прямая будет выше, а для других — ниже функции .
Таблица значений для функции :
При , получаем функцию , которая пересекает ось в точке и ось в точке .
Таблица значений для функции :
Построим графики двух функций:
График функции будет иметь форму угла.
График функции будет прямой, угловой коэффициент которой зависит от значения .
Мы видим, что:
При график прямой будет пересекаться с графиком модуля в одной точке.
При график прямой также пересечется с графиком модуля в одной точке.
При график прямой будет пересекаться с графиком модуля в двух точках, но при графики не пересекаются.
При график прямой будет пересекаться с графиком модуля в одной точке.
Ответ: Уравнение имеет 0 корней при ; 1 корень при .
б) :
Рассмотрим функцию , которая, как и в предыдущем случае, имеет форму угла. Мы можем записать её как:
Таблица значений для функции :
Теперь рассмотрим прямую . Это линейная функция с угловым коэффициентом и пересечением с осью в точке .
При , получаем функцию , которая пересекает ось в точке и ось в точке .
Таблица значений для функции :
При , получаем функцию , которая пересекает ось в точке и ось в точке .
Таблица значений для функции :
Построим графики двух функций:
- График функции будет иметь форму угла.
- График функции будет прямой, угловой коэффициент которой зависит от значения .
Мы видим, что:
- При , график прямой пересекает график модуля в одной точке.
- При , график прямой также пересекает график модуля в одной точке.
- При график прямой будет пересекаться с графиком модуля в двух точках.
- При , график прямой будет пересекаться с графиком модуля в одной точке.
Ответ: Уравнение имеет 1 корень при ; 2 корня при .




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!