
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 497 Дорофеев, Суворова — Подробные Ответы
Используя схематические графики, определите, сколько корней имеет уравнение; укажите два последовательных целых числа, между которыми находятся корни уравнения:
а) ;
б) .
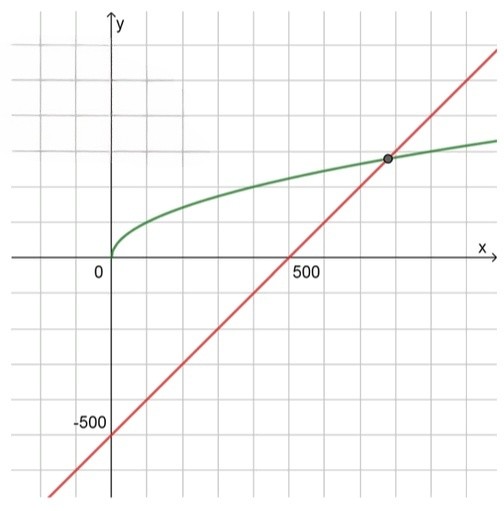
а) :
— уравнение ветви параболы:
, значит функция возрастает;
Вершина находится в точке ;
— уравнение прямой:
, значит функция возрастает;
Пересекает ось в точке с абсциссой ;
Пересекает ось в точке с ординатой ;
3) Схематический рисунок:
Графики пересекаются в одной точке;
4) Найдем промежуток, в котором лежит корень:
и ;
и ;
и ;
и ;
и ;
и ;
и ;
Ответ: 1 корень; .
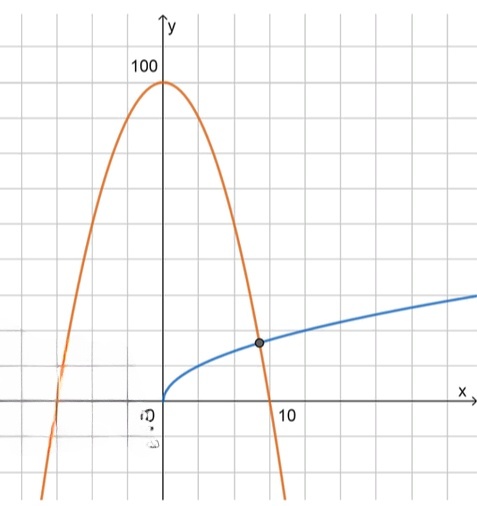
б) :
— уравнение ветви параболы:
, значит функция возрастает;
Вершина находится в точке ;
— уравнение прямой:
, значит функция возрастает;
Вершина находится в точке ;
Пересекает ось в точках с абсциссами ;
Пересекает ось в точке с ординатой ;
3) Схематический рисунок:
Графики пересекаются в одной точке;
4) Найдем промежуток, в котором лежит корень:
и ;
и ;
и ;
Ответ: 1 корень; .
а) :
— уравнение ветви параболы:
Функция представляет собой ветвь параболы, которая определена для . Эта функция возрастает, так как её производная положительна при .
Вершина параболы находится в точке , так как .
— уравнение прямой:
Уравнение представляет собой прямую с угловым коэффициентом , что означает, что прямая возрастает, поскольку её производная .
Прямая пересекает ось в точке , так как при получаем , следовательно, .
Прямая пересекает ось в точке , так как при получаем .
3) Схематический рисунок:
График функции будет представлять собой плавно возрастающую кривую, начинающуюся в точке , а график прямой — это прямая с углом наклона 45° и пересечением с осью в точке .
Графики пересекаются в одной точке, так как уравнение имеет решение.
4) Найдем промежуток, в котором лежит корень:
Для , значение функции и ; очевидно, что на этом промежутке функции равны.
Для , значение и ; функции не равны.
Для , значение и ; функции не равны.
Для , значение и ; функции не равны.
Для , значение и ; функции не равны.
Для , значение и ; функции не равны.
Для , значение и ; функции не равны.
Ответ: 1 корень; .
б) :
— уравнение ветви параболы:
Функция также представляет собой ветвь параболы, которая определяется для и возрастает, так как её производная положительна при .
Вершина параболы находится в точке , так как .
— уравнение параболы:
Это уравнение параболы, направленной вниз, с вершиной в точке , так как при получаем .
Парабола пересекает ось в точках с абсциссами , так как при получаем , следовательно, , то есть .
Парабола пересекает ось в точке .
3) Схематический рисунок:
График функции представляет собой возрастающую кривую, начинающуюся в точке .
График функции — это парабола, направленная вниз, с вершиной в точке .
Графики этих функций пересекаются в одной точке.
4) Найдем промежуток, в котором лежит корень:
Для , значение и ; функции не равны.
Для , значение и ; функции не равны.
Для , значение и ; функции не равны.
Ответ: 1 корень; .




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!