ГДЗ по Алгебре 9 Класс Номер 495 Дорофеев, Суворова — Подробные Ответы

В каком из указанных промежутков находится корень уравнения $\sqrt{x} = 0,5x — 4$?

$(-\infty; 0]$

$[0; 10]$

$[10; 20]$

$[20; +\infty)$

$\sqrt{x} = 0,5x — 4$:

$y = \sqrt{x}$ — уравнение ветви параболы:

$y = 0,5x — 4$ — уравнение прямой:

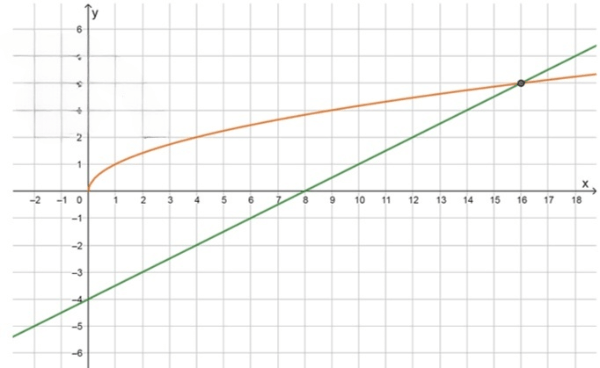
3) Построим графики данных функций:

Графики пересекаются в точке: $(16; 4)$;

Значит, $x = 16$, то есть $x \in [10; 20]$;

Ответ: 3.

1) Уравнение $y = \sqrt{x}$ представляет собой уравнение ветви параболы, которая изображает функцию, определенную на интервале $x \geq 0$, так как $\sqrt{x}$ существует только для неотрицательных значений $x$. Значения $y$ на этом графике будут соответствовать положительным корням из $x$. Для того чтобы построить график этой функции, подставим несколько значений $x$ и найдем соответствующие значения $y$:

• Для $x = 0$, $y = \sqrt{0} = 0$.
• Для $x = 1$, $y = \sqrt{1} = 1$.
• Для $x = 4$, $y = \sqrt{4} = 2$.
• Для $x = 9$, $y = \sqrt{9} = 3$.
• Для $x = 16$, $y = \sqrt{16} = 4$.

Это дает таблицу значений:

График этой функции будет представлять собой ветвь параболы, которая начинается в точке $(0, 0)$ и продолжается вверх, всегда увеличиваясь.

2) Уравнение $y = 0,5x — 4$ представляет собой уравнение прямой. Это линейная функция, коэффициент при $x$ равен $0,5$, а свободный член $-4$ означает, что прямая пересекает ось $y$ в точке $y = -4$. Для построения графика этой функции подставим несколько значений $x$ и найдем соответствующие значения $y$:

• Для $x = 0$, $y = 0,5 \cdot 0 — 4 = -4$.
• Для $x = 8$, $y = 0,5 \cdot 8 — 4 = 0$.

Это дает таблицу значений:

График этой функции будет прямой, которая проходит через точки $(0, -4)$ и $(8, 0)$, и имеет угол наклона $0,5$, что означает, что на каждый шаг по оси $x$ функция увеличивается на $0,5$ единицы по оси $y$.

3) Для нахождения точки пересечения графиков этих двух функций, приравняем их значения:

$$\sqrt{x} = 0,5x — 4$$

Для решения этого уравнения возведем обе части в квадрат:

$$x = (0,5x — 4)^2$$

Раскроем квадрат:

$$x = 0,25x^2 — 4x + 16$$

Переносим все в одну сторону:

$$0,25x^2 — 5x + 16 = 0$$

Умножим все на 4, чтобы избавиться от десятичных коэффициентов:

$$x^2 — 20x + 64 = 0$$

Решаем это квадратное уравнение с помощью дискриминанта:

$$D = (-20)^2 — 4 \cdot 1 \cdot 64 = 400 — 256 = 144$$

Таким образом, корни уравнения будут:

$$x_1=\frac{20+\sqrt{144}}{2}=\frac{20+12}{2}=16$$

$$x_1 = \frac{20 + \sqrt{144}}{2} = \frac{20 + 12}{2} = 16$$ $$x_2 = \frac{20 — \sqrt{144}}{2} = \frac{20 — 12}{2} = 4$$

Теперь проверим, в какой из указанных промежутков находится корень. Поскольку $x_1 = 16$, этот корень принадлежит промежутку $[10; 20]$.

Ответ: 3.