ГДЗ по Алгебре 9 Класс Номер 494 Дорофеев, Суворова — Подробные Ответы

Найдите подбором корень уравнения и, используя графические соображения, докажите, что других корней нет:

а) $\sqrt{x}=12-x$;
б) $x^3+x+10=0$;
в) $x^2+3=\frac{4}{x}$.

а) $\sqrt{x}=12-x$:

1) Найдем корень уравнения подбором:
$\sqrt{1}=1$ и $12-1=11$;
$\sqrt{4}=2$ и $12-2=10$;
$\sqrt{9}=3$ и $12-9=3$;

$\mathrm{2)\; y}=\sqrt{x}$ — уравнение ветви параболы:
$a>0$, значит функция возрастает;
$x_0=0$ и $y_0=0$;

$\mathrm{3)\; y}=12-x$ — уравнение прямой:
$a<0$, значит функция убывает;
$x_0=12$ и $y_0=12$;

4) Схематический рисунок:

Графики пересекаются только в одной точке;
Ответ: $x=9$.

б) $x^3+x+10=0$:
$x^3=-x-10$;

1) Найдем корень уравнения подбором:
$(-1{)}^3=-1$ и $1-10=-9$;
$(-2{)}^3=-8$ и $2-10=-8$;

$\mathrm{2)\; y}=x^3$ — уравнение кубической параболы:
$a>0$, значит функция возрастает;
$x_0=0$ и $y_0=0$;

$\mathrm{3)\; y}=-x-10$ — уравнение прямой:
$a<0$, значит функция убывает;
$x_0=-10$ и $y_0=-10$;

4) Схематический рисунок:

Графики пересекаются только в одной точке;
Ответ: $x=-2$.

в) $x^2+3=\frac{4}{x}$:

1) Найдем корень уравнения подбором:
$1^2+3=4$ и $\frac{4}{1}=4$;

$\mathrm{2)\; y}=x^2+3$ — уравнение параболы:
$a>0$, значит функция возрастает;
$x_0=0$ и $y_0=3$;

$\mathrm{3)\; y}=\frac{4}{x}$ — уравнение гиперболы:
$a>0$, значит функция лежит в I и III четвертях;
$x_0=0$ и $y_0=0$;

4) Схематический рисунок:

Графики пересекаются только в одной точке;
Ответ: $x=1$.

а) $\sqrt{x}=12-x$:

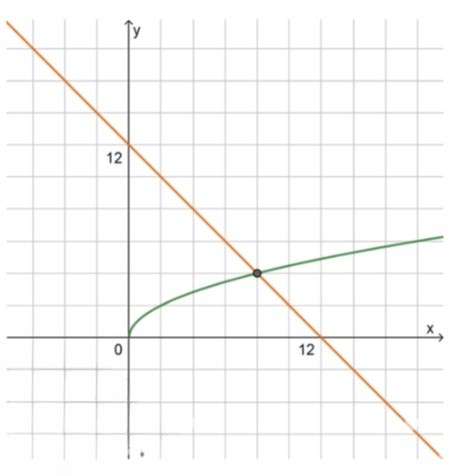
$y=\sqrt{x}$ — уравнение параболы, которая представляет собой ветвь функции $y=\sqrt{x}$, где $a>0$, что указывает на возрастающий характер функции. Функция начинается в точке $(0,0)$, так как $x_0=0$ и $y_0=0$. На графике парабола будет направлена вверх, начиная с начала координат.

$y=12-x$ — уравнение прямой, где коэффициент перед $x$ отрицателен ($a<0$), что говорит о том, что прямая имеет убывающий вид. Прямая пересекает ось $y$ в точке $(0,12)$, так как $x_0=12$ и $y_0=12$, и имеет наклон вниз, направляясь в левую сторону.

При графическом изображении видно, что оба графика пересекаются в одной точке. По наблюдениям за графиками, корень уравнения будет найден в точке пересечения этих двух кривых, где $x=9$. Это значение $x$ является корнем уравнения.

Ответ: $x=9$.

б) $x^3+x+10=0$:

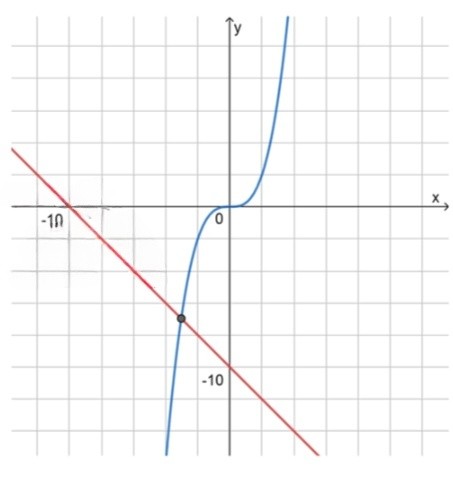
Уравнение $x^3+x+10=0$ может быть переписано как $x^3=-x-10$, что представляет собой уравнение кубической функции. График функции $y=x^3$ будет кубической параболой, где коэффициент при $x^3$ положительный ($a>0$), что говорит о возрастающем поведении функции, которая проходит через точку $(0,0)$, так как $x_0=0$ и $y_0=0$.

Уравнение $y=-x-10$ — это уравнение прямой с отрицательным угловым коэффициентом ($a<0$). Прямая имеет убывающее направление и пересекает ось $y$ в точке $(0,-10)$. Прямая и кубическая парабола пересекаются в одной точке.

Анализируя графики, видно, что они пересекаются в одной точке, что дает нам корень уравнения $x=-2$.

Ответ: $x=-2$.

в) $x^2+3=\frac{4}{x}$:

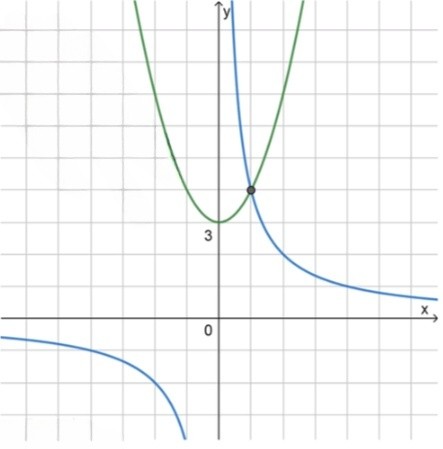
Преобразуем уравнение в форму $x^2-1=-\frac{8}{x}$, что представляет собой уравнение параболы $y=x^2-1$. Это уравнение параболы с минимальной точкой в $(0,-1)$, так как $x_0=0$ и $y_0=-1$. Парабола открывается вверх, так как коэффициент при $x^2$ положительный.

Уравнение $y=\frac{4}{x}$ — это гипербола с двумя ветвями, лежащими в первой и третьей четвертях, так как $a>0$. Гипербола имеет асимптоты на осях координат и начинает приближаться к осям при $x\to \mathrm{\infty }$ или $x\to 0$.

Схематическое изображение этих графиков показывает, что парабола и гипербола пересекаются только в одной точке. После анализа графика мы можем утверждать, что корень уравнения находится в точке $x=1$.

Ответ: $x=1$.