ГДЗ Дорофеев 9 Класс по Алгебре Шарыгин Учебник 📕 Суворова- Все Части

ГДЗ по Алгебре 9 Класс Номер 492 Дорофеев, Суворова - Подробные Ответы

Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. и др.

9 класс

Класс

Предмет

ГДЗ Дорофеев 7, 8, 9 Класс по Алгебре Все Учебники - Ответы на Любые Задачи Бесплатно

Тип

ГДЗ, Решебник.

Автор

Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. и др.

Год

2022.

Издательство

Просвещение.

Описание

Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.

Оцени решение

← Предыдущий Следующий →

Сообщить об ошибке

ГДЗ по Алгебре 9 Класс Номер 492 Дорофеев, Суворова — Подробные Ответы

Задача

С помощью графиков определите, сколько корней имеет уравнение; для каждого корня укажите два целых числа, между которыми он находится:

а) $\frac{1}{x} = x^2 — 4$ ;

б) $x^3 — x — 9 = 0$ .

Краткий ответ

а) $\frac{1}{x} = x^2 — 4$ :

$y = \frac{1}{x}$ — уравнение гиперболы:

$x$	$-2$	$-1$	$-0,5$	$0,5$	$1$	$2$
$y$	$-0,5$	$-1$	$-2$	$2$	$1$	$0,5$

$y = x^2 — 4$ — уравнение параболы:
$x_0 = 0$ и $y_0 = -4$ ;

$x$	$-3$	$-1$	$1$	$3$
$y$	$5$	$-3$	$-3$	$5$

Ответ: $x_1 \in [2; 3]$ ; $x_2 \in [-2; -1]$ ; $x_3 \in [-1; 0]$ .

Подробный ответ

а) $\frac{1}{x} = x^2 — 4$ :

Уравнение $y = \frac{1}{x}$ представляет собой гиперболу. Для построения графика функции подставим различные значения $x$ в уравнение и вычислим соответствующие значения $y$ :

$x$	$-2$	$-1$	$-0,5$	$0,5$	$1$	$2$
$y$	$-0,5$	$-1$	$-2$	$2$	$1$	$0,5$

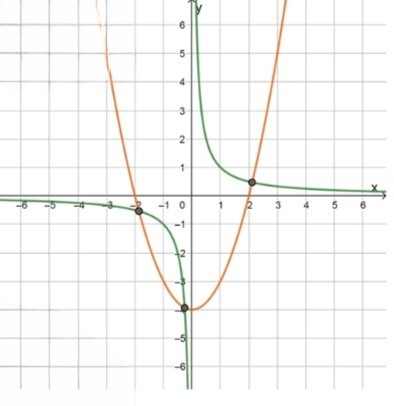
Мы видим, что график функции $y = \frac{1}{x}$ является гиперболой, которая имеет асимптоты $y = 0$ и $x = 0$ . График функции имеет два ответвления, одно в верхней части и одно в нижней. Эта гипербола пересекает ось $y$ в точке, где $x = 0$ , но в этой точке функция не определена.

Уравнение $y = x^2 — 4$ представляет собой параболу. Для построения графика этой функции подставим различные значения $x$ в уравнение и вычислим соответствующие значения $y$ :

$x$	$-3$	$-1$	$1$	$3$
$y$	$5$	$-3$	$-3$	$5$

График функции $y = x^2 — 4$ — это парабола, которая открывается вверх и имеет вершину в точке $(0, -4)$ . Парабола пересекает ось $y$ в точке $y = -4$ , и пересекает ось $x$ в точках, где $y = 0$ , то есть в точках $x = -2$ и $x = 2$ .

Теперь решим уравнение $\frac{1}{x} = x^2 — 4$ . Чтобы найти корни уравнения, приравняем графики двух функций, то есть найдём точки пересечения гиперболы $y = \frac{1}{x}$ и параболы $y = x^2 — 4$ . Для этого решим уравнение:

$\frac{1}{x} = x^2 — 4.$

Умножим обе части уравнения на $x$ (при условии, что $x \neq 0$ ):

$1 = x^3 — 4x.$

Переносим все слагаемые в одну сторону:

$x^3 — 4x — 1 = 0.$

Теперь нужно решить это кубическое уравнение. Визуально на графиках видно, что у уравнения есть три корня: один положительный и два отрицательных. Примерное расположение корней можно определить как: