ГДЗ по Алгебре 9 Класс Номер 491 Дорофеев, Суворова — Подробные Ответы

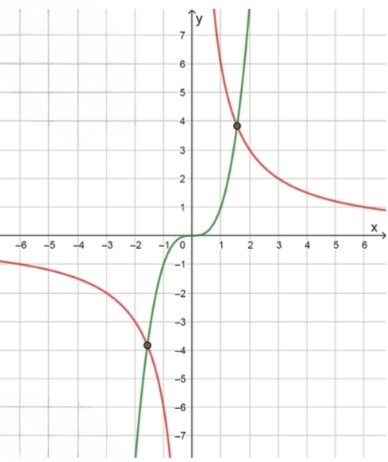
С помощью графиков определите, имеет ли уравнение корни, и если имеет, то сколько. Укажите знаки корней:

а) $x^3 = \frac{6}{x}$;

б) $x^3 = -\frac{1}{x}$;

в) $\sqrt{x} = \frac{1}{x}$;

г) $\sqrt{x} = 1 — x^2$.

а) $x^3 = \frac{6}{x}$:

$y = x^3$ — уравнение кубической параболы:

$y = \frac{6}{x}$ — уравнение гиперболы:

Ответ: 2 корня; положительный и отрицательный.

а) $x^3 = \frac{6}{x}$:

1) Рассмотрим уравнение $y = x^3$. Это уравнение описывает кубическую функцию, график которой представляет собой параболу третьей степени. Подставим различные значения $x$, чтобы построить таблицу значений:

График функции $y = x^3$ пересекает ось $x$ в точке $x = 0$, а для отрицательных значений $x$ функция убывает, и для положительных значений $x$ функция возрастает. Таким образом, функция $y = x^3$ имеет одну точку пересечения с осью $x$, а также одну точку пересечения с графиком другой функции.

2) Теперь рассмотрим уравнение $y = \frac{6}{x}$. Это гиперболическая функция, у которой существует вертикальная асимптота в точке $x = 0$ (где функция не определена) и горизонтальная асимптота $y = 0$. Построим таблицу значений для различных $x$:

График функции $y = \frac{6}{x}$ представляет собой гиперболу с вертикальной асимптотой в точке $x = 0$. График стремится к оси $x$, но никогда не пересекает её. Он также пересекает ось $y$ в точке $y = 6$ при $x = 1$.

Теперь, чтобы найти корни уравнения $x^3 = \frac{6}{x}$, приравняем графики этих двух функций. Это означает, что нужно найти такие значения $x$, при которых значения функции $y = x^3$ совпадают с значениями функции $y = \frac{6}{x}$. Для этого решим уравнение:

$$x^3 = \frac{6}{x}.$$

Умножим обе части уравнения на $x$ (при условии, что $x \neq 0$):

$$x^4 = 6.$$

Теперь извлечем корень четвёртой степени из обеих сторон:

$$x = \pm \sqrt[4]{6}.$$

Поскольку извлечение четвёртой степени даёт два корня (положительный и отрицательный), то решениями уравнения будут:

$$x = \sqrt[4]{6} \approx 1.57 \quad \text{и} \quad x = -\sqrt[4]{6} \approx -1.57.$$

Значит, у уравнения $x^3 = \frac{6}{x}$ два корня: $x \approx 1.57$ и $x \approx -1.57$. Оба корня положительные и отрицательные соответственно.

Ответ: два корня: положительный $x \approx 1.57$ и отрицательный $x \approx -1.57$.