
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 490 Дорофеев, Суворова — Подробные Ответы
Действуем по алгоритму. С помощью графиков определите, сколько корней имеет уравнение, и найдите эти корни:
а) ;
б) ;
в) .
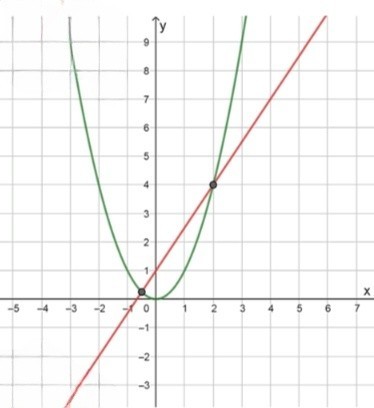
а) :
— уравнение параболы:
и ;
— уравнение прямой:
Уравнение имеет два корня: и ;
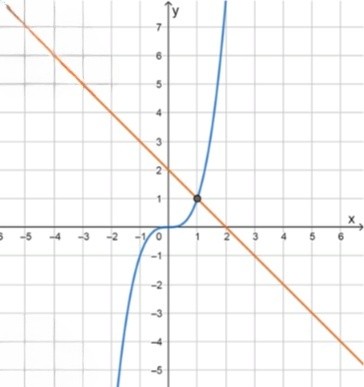
б) :
;
— уравнение кубической параболы:
— уравнение прямой:
Уравнение имеет один корень: ;
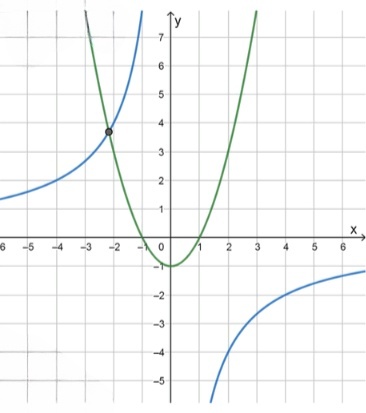
в) :
;
— уравнение параболы:
и ;
— уравнение гиперболы:
и ;
Уравнение имеет один корень: .
а) :
Для начала решим уравнение . Переносим все элементы в одну сторону:
Это квадратное уравнение, которое можно решить с помощью дискриминанта. В стандартной форме , коэффициенты:
Найдем дискриминант :
Дискриминант положительный, значит, у уравнения два действительных корня. Найдем их по формуле:
Таким образом, получаем два корня:
Корни уравнения: и .
б) :
Теперь решим уравнение . Для начала перенесем все слагаемые в одну сторону:
Попробуем применить метод подбора корней. Подставим несколько значений для :
Подставим :
Таким образом, является корнем уравнения.
Чтобы найти другие корни, разделим исходное уравнение на с помощью деления многочленов.
Для деления на используем схематическое деление:
Шаги деления:
Разделим на , получаем .
Умножим на , получаем .
Вычитаем из , получаем .
Разделим на , получаем .
Умножим на , получаем .
Вычитаем из , получаем .
Разделим на , получаем .
Умножим на , получаем .
Вычитаем из , получаем остаток 0.
Таким образом, делится на , и результат деления — это:
Теперь решим квадратное уравнение . Для этого найдем дискриминант:
Так как дискриминант отрицателен, у этого уравнения нет действительных корней. Таким образом, — единственный действительный корень уравнения .
в) :
Для решения уравнения умножим обе части уравнения на (при этом ):
Переносим все слагаемые в одну сторону:
Теперь применим метод подбора. Подставим несколько значений для :
Подставим :
Значит, не является корнем.
Подставим :
Значит, не является корнем.
Попробуем более сложные методы для нахождения корней, например, численный метод или метод Ньютона, чтобы найти приближенные корни.




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!