ГДЗ по Алгебре 9 Класс Номер 472 Дорофеев, Суворова — Подробные Ответы

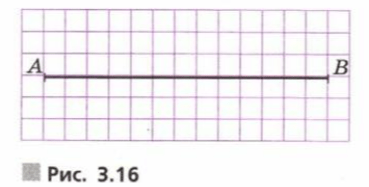
а) Начертите план участка прямоугольной формы, в котором отрезок AB (рис. 3.16) — это дорожка, идущая по диагонали участка. Длина дорожки 13 м, а периметр участка равен 34 м. Сколько решений имеет задача?

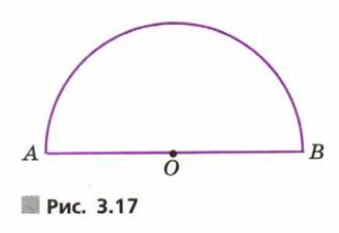
б) На отрезке АВ как на диаметре (рис. 3.17) построена полуокружность. Её радиус равен 10 см. Постройте на полуокружности точку С, такую, чтобы расстояние от этой точки до одного из концов диаметра было на 4 см больше, чем расстояние от этой точки до другого конца диаметра. Сколько решений имеет задача?

а) Пусть одна сторона участка равна $x$ м, а другая — $y$ м.

1) Периметр участка равен 34 м, значит: $x + y = 17$;

2) Длина дорожки (диагонали) равна 13 м, значит: $x^2 + y^2 = 169$;

3) Составим и решим систему уравнений:

$$\begin{cases} x + y = 17 \\ x^2 + y^2 = 169 \end{cases} \Rightarrow \begin{cases} y = 17 — x \\ x^2 + y^2 — 169 = 0 \end{cases}$$

Подставляем $y = 17 — x$ во второе уравнение:

$$x^2 + (17 — x)^2 — 169 = 0;$$

Раскрываем скобки:

$$x^2 + 289 — 34x + x^2 — 169 = 0;$$

Собираем подобные слагаемые:

$$2x^2 — 34x + 120 = 0 \quad | : 2;$$

Делим обе части на 2 для упрощения:

$$x^2 — 17x + 60 = 0;$$

Теперь вычислим дискриминант $D$ для этого квадратного уравнения:

$$D = (-17)^2 — 4 \cdot 1 \cdot 60 = 289 — 240 = 49;$$

Так как дискриминант $D = 49$ является полным квадратом, у уравнения два действительных корня. Находим их с помощью формулы:

$$x_1=\frac{-(-17)-\sqrt{49}}{2\cdot 1}=\frac{17-7}{2}=\frac{10}{2}=5,$$

$$x_1 = \frac{-(-17) — \sqrt{49}}{2 \cdot 1} = \frac{17 — 7}{2} = \frac{10}{2} = 5,$$ $$x_2 = \frac{-(-17) + \sqrt{49}}{2 \cdot 1} = \frac{17 + 7}{2} = \frac{24}{2} = 12.$$

Теперь находим соответствующие значения $y$, подставляя $x_1 = 5$ и $x_2 = 12$ в уравнение $y = 17 — x$:

Для $x_1 = 5$:

$$y_1 = 17 — 5 = 12;$$

Для $x_2 = 12$:

$$y_2 = 17 — 12 = 5.$$

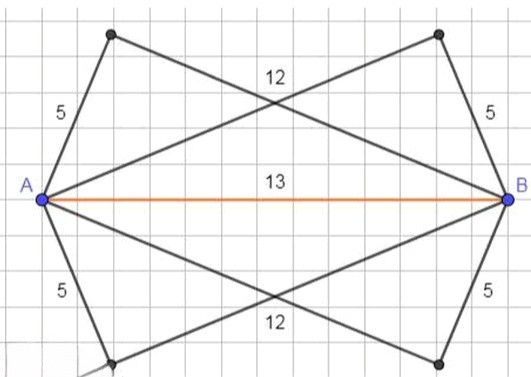
4) Начертим план участка:

Ответ: два решения; 5 метров и 12 метров.

б) Пусть один из отрезков $AC$ и $BC$ равен $x$ см, а другой — $y$ см.

1) Угол $ACB$ вписан в окружность, значит $\Delta ACB$ — прямоугольный. Отрезки $AC$ и $BC$ являются катетами, а отрезок $AB$ — гипотенузой;

2) Радиус полукружности равен 10 см, значит $AB = 2 \cdot 10 = 20$ см;

3) Один из катетов на 4 см больше другого, значит: $x — y = 4$;

4) Составим и решим систему уравнений:

$$\begin{cases} x — y = 4 \\ x^2 + y^2 = 400 \end{cases} \Rightarrow \begin{cases} y = x — 4 \\ x^2 + y^2 — 400 = 0 \end{cases}$$

Подставляем $y = x — 4$ во второе уравнение:

$$x^2 + (x — 4)^2 — 400 = 0;$$

Раскрываем скобки:

$$x^2 + x^2 — 8x + 16 — 400 = 0;$$

Собираем подобные слагаемые:

$$2x^2 — 8x — 384 = 0 \quad | : 2;$$

Делим обе части на 2 для упрощения:

$$x^2 — 4x — 192 = 0;$$

Теперь вычислим дискриминант $D$ для этого квадратного уравнения:

$$D = (-4)^2 — 4 \cdot 1 \cdot (-192) = 16 + 768 = 784 = 28^2;$$

Так как дискриминант $D = 784$ является полным квадратом, у уравнения два действительных корня. Находим их с помощью формулы:

$$x_1=\frac{-(-4)-28}{2\cdot 1}=\frac{4-28}{2}=\frac{-24}{2}=-12,$$

$$x_1 = \frac{-(-4) — 28}{2 \cdot 1} = \frac{4 — 28}{2} = \frac{-24}{2} = -12,$$ $$x_2 = \frac{-(-4) + 28}{2 \cdot 1} = \frac{4 + 28}{2} = \frac{32}{2} = 16.$$

5) Отрезок не может иметь отрицательную длину:

$$x \neq -12, \quad \text{значит } x = 16 \, (\text{см}), \quad \text{тогда } y = 16 — 4 = 12 \, (\text{см});$$

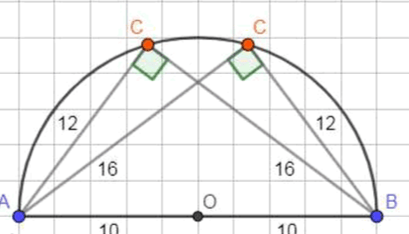
6) Отметим точку $C$ на рисунке:

Ответ: 2 решения; $AC = 16$ см, $BC = 12$ см или $AC = 12$ см, $BC = 16$ см.

а) Пусть одна сторона участка равна $x$ м, а другая — $y$ м.

1) Периметр участка равен 34 м, значит: $x + y = 17$;

Периметр прямоугольника выражается как сумма всех его сторон. Однако, поскольку противоположные стороны прямоугольника равны, то периметр можно выразить через длины двух сторон:

$$x + y = 17.$$

2) Длина дорожки (диагонали) равна 13 м, значит: $x^2 + y^2 = 169$;

Длина диагонали прямоугольного треугольника равна гипотенузе, и по теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов. В данном случае гипотенуза равна 13 см, и мы получаем уравнение:

$$x^2 + y^2 = 169.$$

3) Составим и решим систему уравнений:

$$\begin{cases} x + y = 17 \\ x^2 + y^2 = 169 \end{cases} \Rightarrow \begin{cases} y = 17 — x \\ x^2 + y^2 — 169 = 0 \end{cases}$$

Подставим $y = 17 — x$ из первого уравнения во второе:

$$x^2 + (17 — x)^2 — 169 = 0.$$

Раскрываем скобки:

$$x^2 + 289 — 34x + x^2 — 169 = 0.$$

Приводим подобные слагаемые:

$$2x^2 — 34x + 120 = 0 \quad | : 2;$$

Делим обе части на 2 для упрощения:

$$x^2 — 17x + 60 = 0.$$

Теперь находим дискриминант $D$ для этого квадратного уравнения. Используем формулу для дискриминанта:

$$D = b^2 — 4ac,$$

где $a = 1$, $b = -17$, $c = 60$. Подставляем значения:

$$D = (-17)^2 — 4 \cdot 1 \cdot 60 = 289 — 240 = 49.$$

Так как дискриминант $D = 49$ является полным квадратом, у уравнения два действительных корня. Находим их с помощью формулы для корней квадратного уравнения:

$$x_1=\frac{-(-17)-\sqrt{49}}{2\cdot 1}=\frac{17-7}{2}=\frac{10}{2}=5,$$

$$x_1 = \frac{-(-17) — \sqrt{49}}{2 \cdot 1} = \frac{17 — 7}{2} = \frac{10}{2} = 5,$$ $$x_2 = \frac{-(-17) + \sqrt{49}}{2 \cdot 1} = \frac{17 + 7}{2} = \frac{24}{2} = 12.$$

Теперь находим соответствующие значения $y$, подставляя $x_1 = 5$ и $x_2 = 12$ в уравнение $y = 17 — x$:

Для $x_1 = 5$:

$$y_1 = 17 — 5 = 12;$$

Для $x_2 = 12$:

$$y_2 = 17 — 12 = 5.$$

Ответ: 3 см и 4 см.

б) Пусть один из отрезков $AC$ и $BC$ равен $x$ см, а другой — $y$ см.

1) Угол $ACB$ вписан в окружность, значит $\Delta ACB$ — прямоугольный. Отрезки $AC$ и $BC$ являются катетами, а отрезок $AB$ — гипотенузой;

Это уравнение основано на теореме о прямоугольном треугольнике, вписанном в окружность. Поскольку угол $ACB$ является прямым, то отрезки $AC$ и $BC$ являются катетами прямоугольного треугольника, а отрезок $AB$ является гипотенузой.

2) Радиус полукружности равен 10 см, значит $AB = 2 \cdot 10 = 20$ см;

Радиус полукружности равен половине длины гипотенузы. Таким образом, длина гипотенузы $AB$ равна 20 см, поскольку радиус полукружности равен 10 см.

3) Один из катетов на 4 см больше другого, значит: $x — y = 4$;

Это уравнение описывает разницу в длинах катетов. Один катет на 4 см длиннее другого, поэтому разница между длинами катетов равна 4 см:

$$x — y = 4.$$

4) Составим и решим систему уравнений:

$$\begin{cases} x — y = 4 \\ x^2 + y^2 = 400 \end{cases} \Rightarrow \begin{cases} y = x — 4 \\ x^2 + y^2 — 400 = 0 \end{cases}$$

Подставляем $y = x — 4$ во второе уравнение:

$$x^2 + (x — 4)^2 — 400 = 0.$$

Раскрываем скобки:

$$x^2 + x^2 — 8x + 16 — 400 = 0.$$

Приводим подобные слагаемые:

$$2x^2 — 8x — 384 = 0 \quad | : 2;$$

Делим обе части на 2 для упрощения:

$$x^2 — 4x — 192 = 0.$$

Теперь находим дискриминант $D$ для этого квадратного уравнения:

$$D = (-4)^2 — 4 \cdot 1 \cdot (-192) = 16 + 768 = 784 = 28^2.$$

Так как дискриминант $D = 784$ является полным квадратом, у уравнения два действительных корня. Находим их с помощью формулы:

$$x_1=\frac{-(-4)-28}{2\cdot 1}=\frac{4-28}{2}=\frac{-24}{2}=-12,$$

$$x_1 = \frac{-(-4) — 28}{2 \cdot 1} = \frac{4 — 28}{2} = \frac{-24}{2} = -12,$$ $$x_2 = \frac{-(-4) + 28}{2 \cdot 1} = \frac{4 + 28}{2} = \frac{32}{2} = 16.$$

5) Отрезок не может иметь отрицательную длину:

$$x \neq -12, \quad \text{значит } x = 16 \, (\text{см}), \quad \text{тогда } y = 16 — 4 = 12 \, (\text{см});$$

6) Отметим точку $C$ на рисунке:

Ответ: 2 решения; $AC = 16$ см, $BC = 12$ см или $AC = 12$ см, $BC = 16$ см.