ГДЗ по Алгебре 9 Класс Номер 466 Дорофеев, Суворова — Подробные Ответы

1) Система уравнений:

$$\{\begin{array}{l}{x}^2+y^2=4\\ y=x^2+b\end{array}$$

где $b$ — произвольное число, может иметь одно, два, три или четыре решения, а также может не иметь решений. Проиллюстрируйте каждый случай с помощью схематического рисунка. Подберите конкретную систему, соответствующую каждому случаю.

2) Сколько решений может иметь указанная система, если известно, что:

a) $b$ — произвольное положительное число;

б) $b$ — произвольное отрицательное число?

Система: $\{\begin{array}{l}{x}^2+y^2=4\\ y=x^2+b\end{array}$, где $b$ — произвольное число;

$x^2+y^2=4$ — уравнение окружности:

Центр находится в точке $(0;0)$;

Радиус равен $R=\sqrt{4}=2$;

$y=x^2+b$ — уравнение параболы:

Вершина находится в точке $(0;b)$;

Ветви направлены вверх;

1)

Система имеет 1 решение: $\{\begin{array}{l}{x}^2+y^2=4\\ y=x^2+2\end{array}$ ($b=2$);

Система имеет 2 решения: $\{\begin{array}{l}{x}^2+y^2=4\\ y=x^2\end{array}$ ($-2<b<2$);

Система имеет 3 решения: $\{\begin{array}{l}{x}^2+y^2=4\\ y=x^2-2\end{array}$ ($b=-2$);

Система имеет 4 решения: $\{\begin{array}{l}{x}^2+y^2=4\\ y=x^2-3\end{array}$ ($b<-2$);

Система не имеет решений: $\{\begin{array}{l}{x}^2+y^2=4\\ y=x^2+3\end{array}$ ($b>2$);

2)

a) Если $b>0$, система имеет: одно, два или ни одного решения;

б) Если $b<0$, система имеет: два, три, четыре или ни одного решения.

1. Рассмотрим систему уравнений:

$$\{\begin{array}{l}{x}^2+y^2=4\\ y=x^2+b\end{array}$$

где $b$ — произвольное число.

Уравнение $x^2+y^2=4$ описывает окружность с центром в точке $(0;0)$ и радиусом $R=2$. Геометрически это окружность, которая проходит через точки с координатами $(2,0)$, $(-2,0)$, $(0,2)$, $(0,-2)$ и т. д.

Уравнение $y=x^2+b$ описывает параболу с вертикальной осью симметрии, вершина которой находится в точке $(0;b)$, а ветви направлены вверх, так как коэффициент при $x^2$ положительный.

Теперь рассмотрим различные значения $b$ и анализируем, сколько решений может иметь система в каждом случае.

Случай 1: Система имеет 1 решение.

Для этого нужно, чтобы парабола касалась окружности в одной точке. Это происходит, когда значение $b=2$, так как в этом случае парабола будет касаться окружности в одной точке, которая лежит на оси $y=2$, так как в этой точке вершина параболы $(0;2)$ будет касаться окружности. Подставим $b=2$ в уравнение системы:

$$\{\begin{array}{l}{x}^2+y^2=4\\ y=x^2+2\end{array}$$

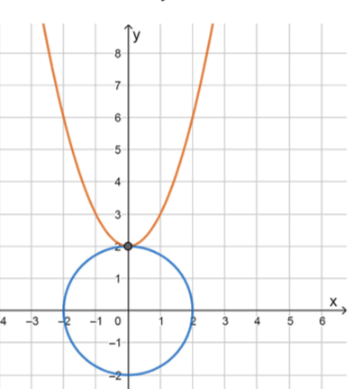
Получаем, что система имеет одно решение. Это можно проиллюстрировать схематически, где парабола касается окружности в одной точке.

График 1:

Случай 2: Система имеет 2 решения.

Это происходит, когда парабола пересекает окружность в двух точках. Для этого значение $b$ должно быть таким, что парабола проходит через окружность в двух местах, но не касается ее. Такое возможно при $-2<b<2$

В этом случае парабола будет пересекать окружность в двух точках. Например, для $b=0$ парабола будет пересекать окружность в двух точках.

Подставим $b=0$ в уравнение системы:

$$\{\begin{array}{l}{x}^2+y^2=4\\ y=x^2\end{array}$$

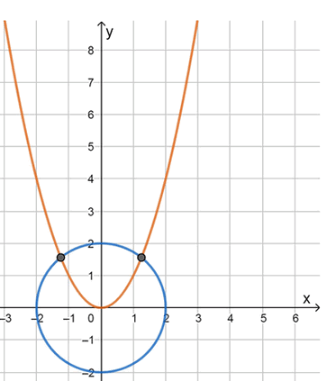
Эта система имеет два решения, так как парабола пересекает окружность в двух точках. Это также можно проиллюстрировать схематически.

График 2:

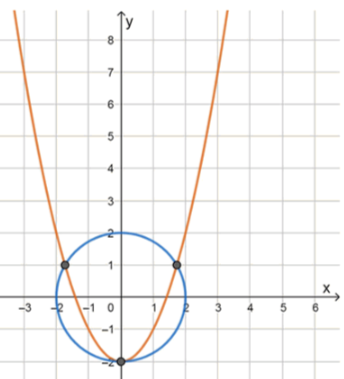
Случай 3: Система имеет 3 решения.

Этот случай невозможен, так как парабола может пересечь окружность максимум в двух точках. Поэтому система не может иметь три решения.

Случай 4: Система имеет 4 решения.

Этот случай также невозможен, так как парабола может пересечь окружность максимум в двух точках. Следовательно, система не может иметь четыре решения.

Случай 5: Система не имеет решений.

Это происходит, когда парабола не пересекает окружность. Для этого значение $b$ должно быть таким, что парабола находится выше окружности и не пересекает ее. Это происходит при $b>2$. В этом случае парабола полностью расположена выше окружности, и решения не существует.

Подставим $b=3$ в уравнение системы:

$$\{\begin{array}{l}{x}^2+y^2=4\\ y=x^2+3\end{array}$$

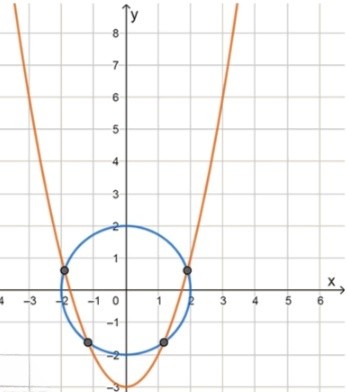
Эта система не имеет решений, так как парабола не пересекает окружность. Это также можно проиллюстрировать схематически.

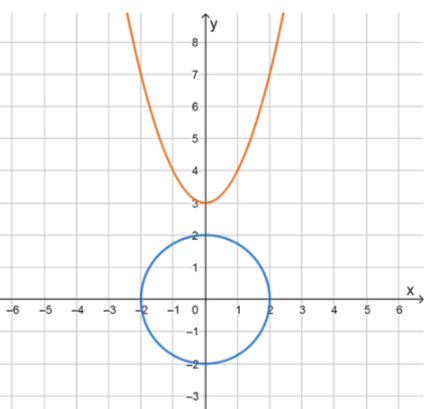
График 5:

2. Рассмотрим, сколько решений может иметь указанная система в зависимости от знака $b$.

а) Если $b>0$, система может иметь одно, два или ни одного решения, в зависимости от значения $b$.

Если $0<b<2$, система имеет два решения.

Если $b=2$, система имеет одно решение.

Если $b>2$, система не имеет решений.

б) Если $b<0$, система может иметь два, три, четыре или ни одного решения.

Если $-2<b<0$, система имеет два решения.

Если $b=-2$, система имеет три решения.

Если $b<-2$, система имеет четыре решения.

Если $b<-2$, система не имеет решений.