ГДЗ по Алгебре 9 Класс Номер 464 Дорофеев, Суворова — Подробные Ответы

Парабола $y = ax^2 + bx + c$ проходит через точки $M(0; 1)$, $N(1; 0)$ и $K(3; 10)$. Задайте эту параболу уравнением и постройте её.

Указание. В качестве образца воспользуйтесь примером 5.

Парабола: $y = ax^2 + bx + c$;

Точки: $M(0; 1)$, $N(1; 0)$, $K(3; 10)$;

1) Составим систему уравнений:

$\begin{cases} 1 = a \cdot 0^2 + b \cdot 0 + c \\ 0 = a \cdot 1^2 + b \cdot 1 + c \\ 10 = a \cdot 3^2 + b \cdot 3 + c \end{cases} \Rightarrow \begin{cases} c = 1 \\ a + b + 1 = 0 \\ 9a + 3b + 1 = 10 \end{cases}$

2) $\{\begin{array}{l}3a+3b+3=0\\ 9a+3b+1=10\end{array}$$\begin{cases} 3a + 3b + 3 = 0 \\ 9a + 3b + 1 = 10 \end{cases}$

$3a — 9a + 3b — 3b + 3 — 1 = 0 — 10;$

$-6a + 2 = -10;$

$-6a = -12, \text{ отсюда } a = 2;$

$a + b + 1 = 0;$

$b = -a — 1;$

$b = -2 — 1 = -3;$

4) Запишем уравнение и построим его график:

$y = 2x^2 — 3x + 1;$

Вершина находится в точке с координатами:

$x_0 = -\frac{-3}{2 \cdot 2} = \frac{3}{4}$ и $y_0 = \frac{4 \cdot 2 \cdot 1 — 3^2}{4 \cdot 2} = \frac{8 — 9}{8} = -\frac{1}{8};$

Координаты некоторых точек:

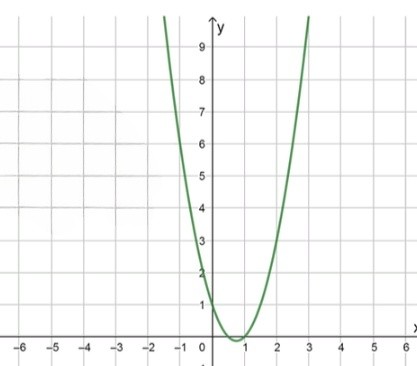
График функции:

Ответ: $y = 2x^2 — 3x + 1$.

Составляем систему уравнений для нахождения коэффициентов параболы, проходящей через точки $M(0, 1)$, $N(1, 0)$ и $K(3, 10)$:

Уравнение параболы имеет вид $y = ax^2 + bx + c$.

Для точки $M(0, 1)$, подставляем $x = 0$ и $y = 1$:

$$1 = a \cdot 0^2 + b \cdot 0 + c \quad \Rightarrow \quad c = 1.$$

Для точки $N(1, 0)$, подставляем $x = 1$ и $y = 0$:

$$0 = a \cdot 1^2 + b \cdot 1 + c \quad \Rightarrow \quad a + b + c = 0 \quad \Rightarrow \quad a + b + 1 = 0 \quad \Rightarrow \quad a + b = -1.$$

Для точки $K(3, 10)$, подставляем $x = 3$ и $y = 10$:

$$10 = a \cdot 3^2 + b \cdot 3 + c \quad \Rightarrow \quad 9a + 3b + 1 = 10 \quad \Rightarrow \quad 9a + 3b = 9.$$

Получаем систему уравнений:

$$\begin{cases} c = 1, \\ a + b = -1, \\ 9a + 3b = 9. \end{cases}$$

Упростим систему уравнений:

$$\begin{cases} a + b = -1, \\ 9a + 3b = 9. \end{cases}$$

Для удобства умножим первое уравнение на 3:

$$3a + 3b = -3.$$

Теперь вычитаем из второго уравнения первое:

$$(9a + 3b) — (3a + 3b) = 9 — (-3),$$

получаем:

$$6a = 12 \quad \Rightarrow \quad a = 2.$$

Подставляем найденное значение $a = 2$ в уравнение $a + b = -1$:

$$2 + b = -1 \quad \Rightarrow \quad b = -1 — 2 = -3.$$

Таким образом, коэффициенты параболы: $a = 2$, $b = -3$, $c = 1$. Уравнение параболы:

$$y = 2x^2 — 3x + 1.$$

Найдем вершину параболы. Формула для координаты вершины по $x$:

$$x_0 = -\frac{b}{2a} = -\frac{-3}{2 \cdot 2} = \frac{3}{4}.$$

Теперь находим координату $y_0$, подставляя $x_0 = \frac{3}{4}$ в уравнение параболы:

$$y_0 = 2 \left( \frac{3}{4} \right)^2 — 3 \cdot \frac{3}{4} + 1 = 2 \cdot \frac{9}{16} — \frac{9}{4} + 1 = \frac{18}{16} — \frac{36}{16} + \frac{16}{16} = -\frac{1}{8}.$$

Таким образом, вершина параболы имеет координаты $\left( \frac{3}{4}, -\frac{1}{8} \right)$.

Построим таблицу значений функции для некоторых $x$:

$$\begin{array}{|c|c|c|c|c|c|} \hline x & -1 & 0 & 1 & 2 & 3 \\ \hline y & 6 & 1 & 0 & 3 & 10 \\ \hline \end{array}$$

График функции имеет форму параболы, направленной вверх.

Ответ: $y = 2x^2 — 3x + 1$.