ГДЗ по Алгебре 9 Класс Номер 455 Дорофеев, Суворова — Подробные Ответы

С помощью графиков определите, сколько решений имеет система уравнений. Укажите приближённо её решения.

а) $\{\begin{array}{l}{x}^2+y^2=4\\ x^2+2x=2-y\end{array}$

б) $\{\begin{array}{l}{x}^2+y^2=25\\ y+5=2x^2-4x\end{array}$

а) $\{\begin{array}{l}{x}^2+y^2=4\\ x^2+2x=2-y\end{array}\Rightarrow \{\begin{array}{l}{x}^2+y^2=4\\ y=-x^2-2x+2\end{array}$

${\mathrm{1)\; x}}^2+y^2=4$ — уравнение окружности:

$x_0=0$ и $y_0=0$, $R=\sqrt{4}=2$;

$\mathrm{2)\; y}=-x^2-2x+2$ — уравнение параболы:

$x_0=-\frac{-2}{-2}=-1$ и $y_0=-(-1{)}^2-2\cdot (-1)+2=3$;

Система имеет 2 решения: $(0;2)$ и $(1,1;-1,6)$.

б) $\{\begin{array}{l}{x}^2+y^2=25\\ y+5=2x^2-4x\end{array}\Rightarrow \{\begin{array}{l}{x}^2+y^2=25\\ y=2x^2-4x-5\end{array}$

${\mathrm{1)\; x}}^2+y^2=25$ — уравнение окружности:

$x_0=0$ и $y_0=0$, $R=\sqrt{25}=5$;

$\mathrm{2)\; y}=2x^2-4x-5$ — уравнение параболы:

$x_0=-\frac{-4}{2\cdot 2}=1$ и $y_0=2\cdot 1^2-4\cdot 1-5=-7$;

Система имеет 4 решения: $(-1,4;4,8)$, $(0;-5)$, $(2,1;-4,5)$ и $(3,3;3,7)$.

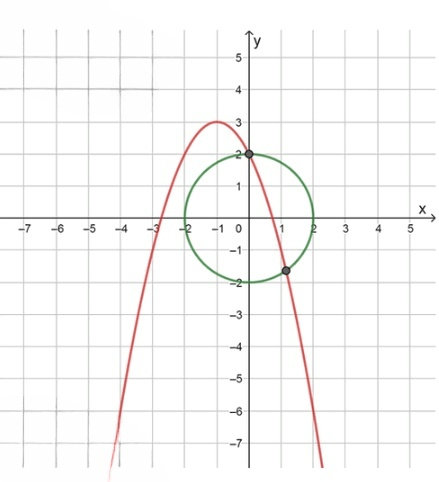
а) $\{\begin{array}{l}{x}^2+y^2=4\\ x^2+2x=2-y\end{array}\Rightarrow \{\begin{array}{l}{x}^2+y^2=4\\ y=-x^2-2x+2\end{array}$

${\mathrm{1)\; x}}^2+y^2=4$ — уравнение окружности. Это уравнение описывает окружность с центром в начале координат и радиусом, равным $R=2$, так как $R=\sqrt{4}=2$. Геометрически это означает, что все точки, которые находятся на расстоянии 2 от начала координат, удовлетворяют данному уравнению. Для различных значений $x$ получаем соответствующие значения $y$. Например:

Это уравнение окружности, которая симметрична относительно обеих осей $x$ и $y$, и пересекает оси в точках $(2,0)$, $(-2,0)$, $(0,2)$, и $(0,-2)$.

$\mathrm{2)\; y}=-x^2-2x+2$ — уравнение параболы. Это уравнение представляет собой параболу, открывающуюся вниз, так как коэффициент при $x^2$ отрицателен. Вершина параболы находится в точке, где $x=-\frac{-2}{2\cdot (-1)}=-1$. Подставив $x=-1$ в уравнение параболы, находим $y_0=-(-1{)}^2-2\cdot (-1)+2=3$. Таким образом, вершина параболы находится в точке $(-1,3)$. Строя таблицу значений для $x$, получаем:

Это уравнение описывает параболу, которая симметрична относительно вертикальной линии $x=-1$. График параболы проходит через точку $(-1,3)$, и значения $y$ становятся все более отрицательными, по мере того как $\mathrm{\mid }x\mathrm{\mid }$ увеличивается.

Ответ: 2 решения. Точки пересечения окружности и параболы могут быть найдены решением системы. Пересечение происходит в точках $(0,2)$ и $(1,1;-1,6)$.

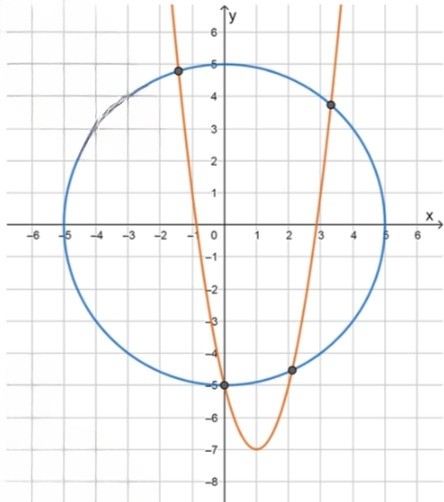
б) $\{\begin{array}{l}{x}^2+y^2=25\\ y+5=2x^2-4x\end{array}\Rightarrow \{\begin{array}{l}{x}^2+y^2=25\\ y=2x^2-4x-5\end{array}$

${\mathrm{1)\; x}}^2+y^2=25$ — уравнение окружности. Это уравнение описывает окружность с центром в начале координат и радиусом $R=\sqrt{25}=5$. Геометрически эта окружность охватывает все точки, которые находятся на расстоянии 5 от начала координат. Строя таблицу значений для $x$, получаем соответствующие значения $y$. Например:

Эта окружность пересекает оси $x$ и $y$ в точках $(5,0)$, $(-5,0)$, $(0,5)$, и $(0,-5)$.

$\mathrm{2)\; y}=2x^2-4x-5$ — уравнение параболы. Это уравнение описывает параболу, открывающуюся вверх, так как коэффициент при $x^2$ положительный. Вершина параболы находится в точке, где $x=-\frac{-4}{2\cdot 2}=1$. Подставив $x=1$ в уравнение параболы, находим $y_0=2\cdot 1^2-4\cdot 1-5=-7$. Таким образом, вершина параболы находится в точке $(1,-7)$. Строя таблицу значений для $x$, получаем:

Эта парабола симметрична относительно вертикальной линии $x=1$. При значении $x=0$, $y=-5$, и с увеличением $x$, $y$ также увеличивается.

Ответ: 4 решения. Точки пересечения окружности и параболы могут быть найдены решением системы. Пересечение происходит в точках $(-1,4;4,8)$, $(0,-5)$, $(2,1;-4,5)$ и $(3,3;3,7)$.