
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 454 Дорофеев, Суворова — Подробные Ответы
Решите графически систему уравнений:
а)
б)
в)
а)
— уравнение параболы:
и ;
| -2 | -1 | 1 | 2 | |
|---|---|---|---|---|
| 6 | 3 | 3 | 6 |
— уравнение гиперболы:
и ;
| -4 | -2 | -1 | 1 | 2 | 4 | |
|---|---|---|---|---|---|---|
| 1 | 2 | 4 | -4 | -2 | -1 |
Ответ: .
б)
— уравнение параболы:
и ;
| -3 | -2 | -1 | 1 | 2 | 3 | |
|---|---|---|---|---|---|---|
| 7 | 2 | -1 | -1 | 2 | 7 |
— уравнение кубической параболы:
| -2 | -1 | 0 | 1 | 2 | |
|---|---|---|---|---|---|
| -8 | -1 | 0 | 1 | 8 |
Ответ: .
в)
— уравнение параболы:
и ;
| -1 | 0 | 1 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| -5 | 0 | 3 | 3 | 0 | -5 |
— уравнение ветви параболы:
| -1 | 0 | 1 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| -5 | 0 | 3 | 3 | 0 | -5 |
Ответ: , и .
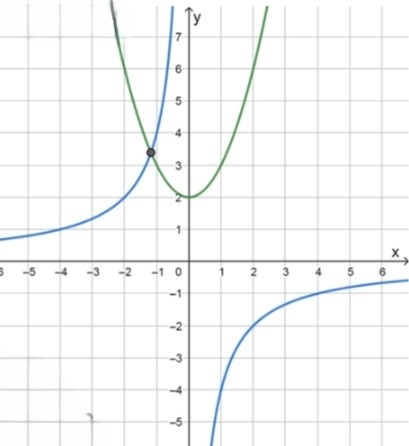
а)
— уравнение параболы. Это уравнение описывает параболу, которая открывается вверх с вершиной в точке . Для различных значений находим соответствующие значения :
| -2 | -1 | 1 | 2 | |
|---|---|---|---|---|
| 6 | 3 | 3 | 6 |
Здесь видно, что парабола симметрична относительно оси , и при , . Парабола растет как для положительных, так и для отрицательных значений .
— уравнение гиперболы. Это уравнение описывает гиперболу, которая имеет асимптоты на осях и , и симметрична относительно начала координат. Для различных значений находим соответствующие значения :
| -4 | -2 | -1 | 1 | 2 | 4 | |
|---|---|---|---|---|---|---|
| 1 | 2 | 4 | -4 | -2 | -1 |
График гиперболы имеет вертикальную асимптоту на оси и горизонтальную на оси , при этом график будет стремиться к этим асимптотам, но никогда не будет их пересекать.
Ответ: . Это точка пересечения параболы и гиперболы, полученная решением системы уравнений.
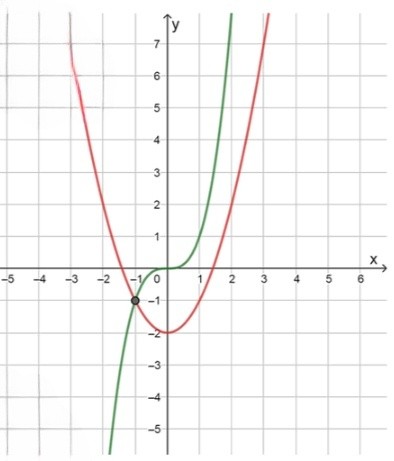
б)
— уравнение параболы. Это уравнение описывает стандартную параболу, которая открывается вверх и имеет вершину в точке . Для разных значений находим соответствующие значения :
| -3 | -2 | -1 | 1 | 2 | 3 | |
|---|---|---|---|---|---|---|
| 7 | 2 | -1 | -1 | 2 | 7 |
Это классическая парабола, которая имеет ось симметрии на оси . Парабола движется вверх при увеличении значения и симметрична относительно вертикальной линии, проходящей через .
— уравнение кубической параболы. Это уравнение представляет кубическую параболу с началом в точке , которая растет быстрее, чем стандартная парабола. Для различных значений находим значения :
| -2 | -1 | 0 | 1 | 2 | |
|---|---|---|---|---|---|
| -8 | -1 | 0 | 1 | 8 |
График этой функции имеет форму, напоминающую «S», и увеличивается быстрее, чем квадратичная парабола. При , , а при больших значениях , также быстро увеличивается.
Ответ: . Это точка пересечения параболы и кубической параболы, полученная решением системы уравнений.
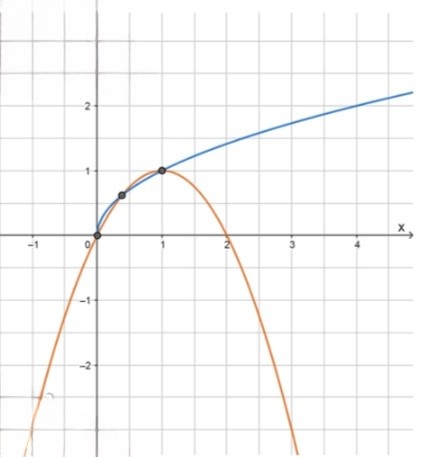
в)
— уравнение параболы. Это уравнение представляет параболу, которая открывается вниз. Вершина параболы находится в точке , и она симметрична относительно оси . Для разных значений находим соответствующие значения :
| -1 | 0 | 1 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| -5 | 0 | 3 | 3 | 0 | -5 |
Этот график параболы показывает, что она убывает слева от вершины и возрастает справа, при этом имеет ось симметрии на .
— уравнение ветви параболы. Это уравнение представляет ветвь параболы, которая существует только для неотрицательных значений . Для различных значений находим соответствующие значения :
| -1 | 0 | 1 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| -5 | 0 | 3 | 3 | 0 | -5 |
Эта функция описывает положительную ветвь параболы, которая начинается с точки и растет с увеличением .
Ответ: , и . Это три точки пересечения параболы и ветви параболы, которые можно найти при решении системы уравнений.




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!