
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 452 Дорофеев, Суворова — Подробные Ответы
;
;
;
;
;
.
Рассмотрим данное уравнение . Это выражение является разностью квадратов, и его можно разложить на множители:
Теперь, чтобы это произведение равнялось нулю, одно из множителей должно быть равно нулю. Таким образом, у нас есть два случая:
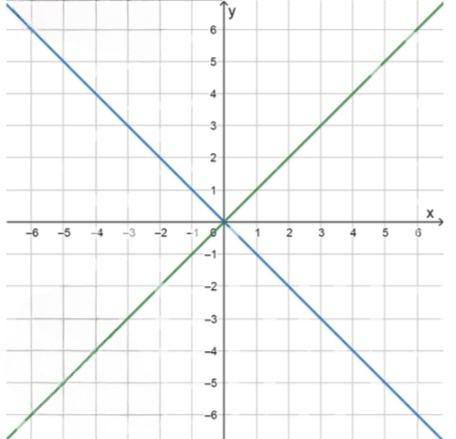
, что приводит к . Это уравнение представляет собой прямую, на которой значения и равны между собой. Строя таблицу значений для и , получаем:
, что приводит к . Это уравнение также представляет прямую, но с угловым коэффициентом, равным . Строя таблицу значений для и , получаем:
Рассмотрим уравнение . Переносим все выражения на одну сторону, получаем:
Это уравнение также является разностью квадратов и может быть разложено на множители:
Снова, чтобы это произведение равнялось нулю, одно из множителей должно быть равно нулю. Таким образом, у нас есть два случая:
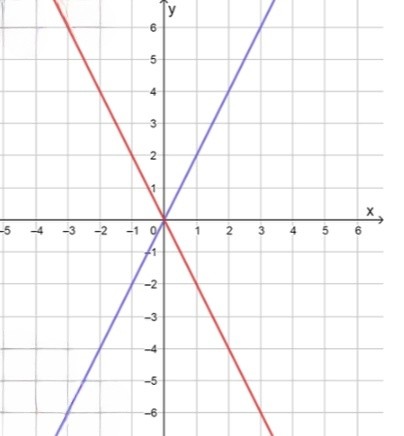
, что приводит к . Это уравнение представляет прямую с угловым коэффициентом, равным 2. Строя таблицу значений для и , получаем:
, что приводит к . Это уравнение представляет прямую с угловым коэффициентом, равным . Строя таблицу значений для и , получаем:
Рассмотрим уравнение . Это уравнение выполняется, если хотя бы одно из переменных равно нулю. Таким образом, есть два случая:
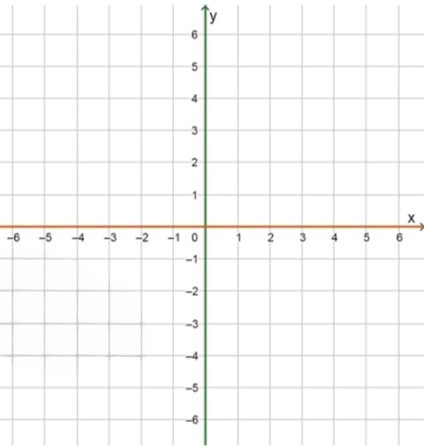
, что представляет собой прямую, на которой всегда равно нулю, а может быть любым значением.
, что представляет собой прямую, на которой всегда равно нулю, а может быть любым значением.
Рассмотрим уравнение . Для того чтобы произведение было равно нулю, хотя бы один из множителей должен быть равен нулю. Таким образом, у нас есть два случая:
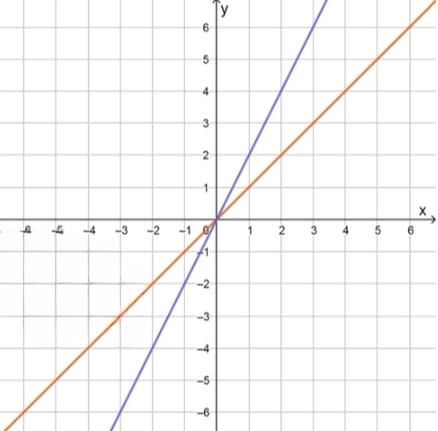
, что приводит к . Это уравнение представляет собой прямую, на которой и равны между собой. Строя таблицу значений для и , получаем:
, что приводит к . Это уравнение представляет прямую с угловым коэффициентом, равным 2. Строя таблицу значений для и , получаем:
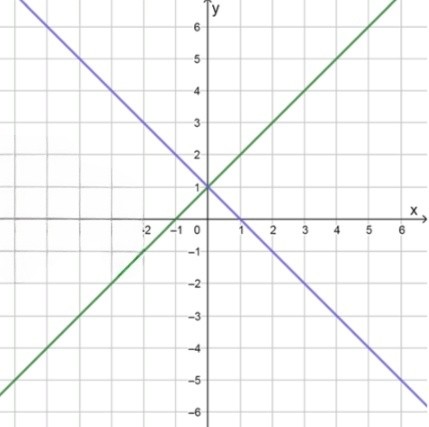
Рассмотрим уравнение . Для того чтобы произведение было равно нулю, хотя бы один из множителей должен быть равен нулю. Таким образом, у нас есть два случая:
, что приводит к . Это уравнение представляет прямую с угловым коэффициентом 1. Строя таблицу значений для и , получаем:
, что приводит к . Это уравнение представляет прямую с угловым коэффициентом . Строя таблицу значений для и , получаем:
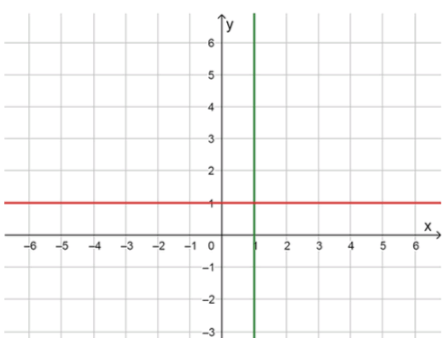
Рассмотрим уравнение . Для того чтобы произведение было равно нулю, хотя бы один из множителей должен быть равен нулю. Таким образом, у нас есть два случая:
, что приводит к . Это уравнение представляет вертикальную прямую на .
, что приводит к . Это уравнение представляет горизонтальную прямую на .




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!