ГДЗ по Алгебре 9 Класс Номер 450 Дорофеев, Суворова — Подробные Ответы

Изобразите схематически графики заданных функций и определите, пересекаются ли они. Если да, то найдите координаты точек пересечения этих графиков.

$y = 2x — 4$ и $y = \frac{6}{x};$

$y = \frac{6}{x}$ и $y = -2x;$

$y = 2x — 4$ и $y = \frac{6}{x};$

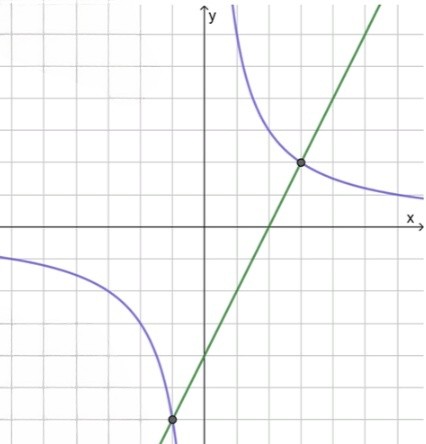
$y = 2x — 4$ — уравнение прямой:

$a > 0$, значит функция возрастает;

График пересекает ось $y$ в точке $(0; -4);$

$y = \frac{6}{x}$ — уравнение гиперболы:

Асимптоты заданы уравнениями $x = 0$ и $y = 0;$

$a > 0$, значит график лежит в I и III четвертях;

3) Найдем координаты точек пересечения:

$2x — 4 = \frac{6}{x} \quad | \cdot x;$

$2x^2 — 4x = 6;$

$2x^2 — 4x — 6 = 0 \quad | : 2;$

$x^2 — 2x — 3 = 0;$

$D = 2^2 + 4 \cdot 3 = 4 + 12 = 16,$ тогда:

$x_1 = \frac{2 — 4}{2} = -1$ и $x_2 = \frac{2 + 4}{2} = 3;$

$y_1 = \frac{6}{-1} = -6$ и $y_2 = \frac{6}{3} = 2;$

Ответ: пересекаются в точках $(3; 2)$ и $(-1; -6).$

б) $y = \frac{6}{x}$ и $y = -2x;$

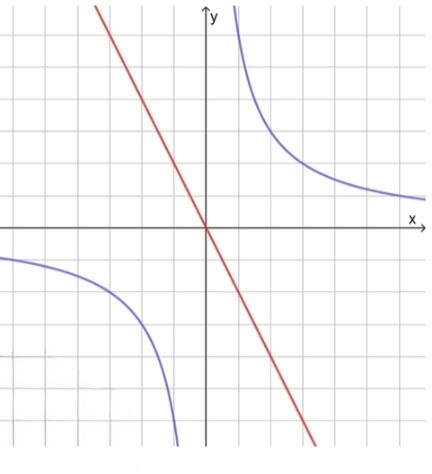
$y = \frac{6}{x}$ — уравнение гиперболы:

Асимптоты заданы уравнениями $x = 0$ и $y = 0;$

$a > 0$, значит график лежит в I и III четвертях;

$y = -2x$ — уравнение прямой:

$a < 0$, значит функция убывает;

График пересекает ось $y$ в точке $(0; 0);$

3) Схематический рисунок:

Ответ: не пересекаются.

$y = 2x — 4$ и $y = \frac{6}{x};$

$y = 2x — 4$ — уравнение прямой:

Определим коэффициент наклона прямой, который равен $a = 2$, это значит, что прямая возрастает, так как $a > 0$.

График прямой пересекает ось $y$ в точке $(0; -4)$, так как при $x = 0$, $y = -4$.

$y = \frac{6}{x}$ — уравнение гиперболы:

Асимптоты гиперболы задаются уравнениями $x = 0$ и $y = 0$, что означает, что график приближается к осям, но не пересекает их.

Параметр $a > 0$ указывает на то, что график гиперболы будет расположен в I и III четвертях, так как $x$ и $y$ имеют одинаковый знак в этих четвертях.

Найдем координаты точек пересечения:

Подставим уравнение $y = 2x — 4$ в уравнение $y = \frac{6}{x}$:

$$2x — 4 = \frac{6}{x} \quad | \cdot x;$$

Умножаем обе стороны на $x$, чтобы избавиться от дроби:

$$2x^2 — 4x = 6;$$

Переносим все на одну сторону:

$$2x^2 — 4x — 6 = 0 \quad | : 2;$$

Разделим на 2:

$$x^2 — 2x — 3 = 0;$$

Решаем полученное квадратное уравнение с использованием дискриминанта:

$$D = (-2)^2 — 4 \cdot 1 \cdot (-3) = 4 + 12 = 16;$$

Находим корни уравнения:

$$x_1=\frac{-(-2)-\sqrt{16}}{2\cdot 1}=\frac{2-4}{2}=-1;$$

$$x_1 = \frac{-(-2) — \sqrt{16}}{2 \cdot 1} = \frac{2 — 4}{2} = -1;$$ $$x_2 = \frac{-(-2) + \sqrt{16}}{2 \cdot 1} = \frac{2 + 4}{2} = 3;$$

Подставляем найденные значения $x_1 = -1$ и $x_2 = 3$ в уравнение $y = 2x — 4$:

$$y_1 = 2 \cdot (-1) — 4 = -2 — 4 = -6;$$ $$y_2 = 2 \cdot 3 — 4 = 6 — 4 = 2;$$

Ответ: пересекаются в точках $(3; 2)$ и $(-1; -6)$.

б) $y = \frac{6}{x}$ и $y = -2x;$

$y = \frac{6}{x}$ — уравнение гиперболы:

Асимптоты гиперболы заданы уравнениями $x = 0$ и $y = 0$, что означает, что график гиперболы приближается к осям, но не пересекает их.

Параметр $a > 0$ указывает, что график гиперболы расположен в I и III четвертях, так как $x$ и $y$ имеют одинаковый знак в этих четвертях.

$y = -2x$ — уравнение прямой:

Коэффициент наклона прямой равен $a = -2$, что означает, что прямая убывает, так как $a < 0$.

Прямая пересекает ось $y$ в точке $(0; 0)$, так как при $x = 0$, $y = 0$.

Схематический рисунок:

Ответ: не пересекаются.