ГДЗ по Алгебре 9 Класс Номер 443 Дорофеев, Суворова — Подробные Ответы

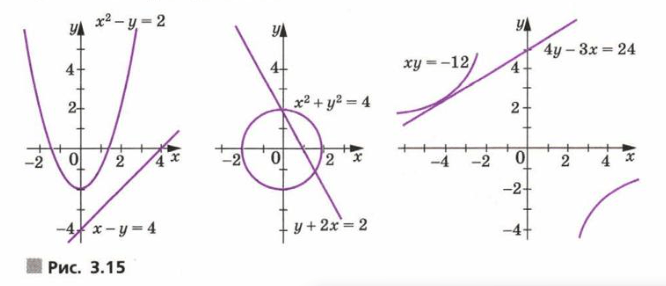
Пользуясь рисунком 3.15, составьте систему уравнений:
1) имеющую два решения;
2) имеющую одно решение;
3) не имеющую решений.

1) Система имеет два решения:
$\begin{cases} x^2 + y^2 = 4 \\ y + 2x = 2 \end{cases}$

2) Система имеет одно решение:
$\begin{cases} xy = -12 \\ 4y — 3x = 24 \end{cases}$

3) Система не имеет решений:
$\begin{cases} x — y = 4 \\ x^2 — y = 2 \end{cases}$

1) Система имеет два решения:
$\begin{cases} x^2 + y^2 = 4 \\ y + 2x = 2 \end{cases}$

Выразим $y$ из второго уравнения:
$y = 2 — 2x$

Подставим это выражение во второе уравнение:
$x^2 + (2 — 2x)^2 = 4$

Вычислим квадрат:
$(2 — 2x)^2 = 4 — 8x + 4x^2$

Подставим:
$x^2 + 4 — 8x + 4x^2 = 4$

Приведём подобные:
$5x^2 — 8x + 4 = 4$

Вычтем 4 из обеих частей:
$5x^2 — 8x = 0$

Вынесем $x$ за скобку:
$x(5x — 8) = 0$

Решения:
$x_1 = 0$, $x_2 = \frac{8}{5}$

Найдём $y$:
Если $x = 0$, то $y = 2 — 0 = 2$
Если $x = \frac{8}{5}$, то $y = 2 — 2 \cdot \frac{8}{5} = 2 — \frac{16}{5} = -\frac{6}{5}$

Ответ: два решения — $(0;2)$ и $\left(\frac{8}{5}; -\frac{6}{5}\right)$

2) Система имеет одно решение:
$\begin{cases} xy = -12 \\ 4y — 3x = 24 \end{cases}$

Выразим $y$ из первого уравнения:
$y = \frac{-12}{x}$

Подставим во второе уравнение:
$4 \cdot \frac{-12}{x} — 3x = 24$

Умножим:
$\frac{-48}{x} — 3x = 24$

Умножим обе части на $x$, чтобы избавиться от дроби:
$-48 — 3x^2 = 24x$

Переносим всё в одну часть:
$-3x^2 — 24x — 48 = 0$

Домножим на $-1$:
$3x^2 + 24x + 48 = 0$

Разделим на 3:
$x^2 + 8x + 16 = 0$

Дискриминант:
$D = 64 — 4 \cdot 1 \cdot 16 = 64 — 64 = 0$

Один корень:
$x = \frac{-8}{2} = -4$

Найдём $y$:
$y = \frac{-12}{-4} = 3$

Ответ: одно решение — $(-4;3)$

3) Система не имеет решений:
$\begin{cases} x — y = 4 \\ x^2 — y = 2 \end{cases}$

Выразим $x$ из первого уравнения:
$x = y + 4$

Подставим во второе:
$(y + 4)^2 — y = 2$

Раскроем скобки:
$y^2 + 8y + 16 — y = 2$

Упростим:
$y^2 + 7y + 16 = 2$

Вычтем 2:
$y^2 + 7y + 14 = 0$

Дискриминант:
$D = 49 — 4 \cdot 1 \cdot 14 = 49 — 56 = -7$

Дискриминант отрицательный, вещественных решений нет

Ответ: решений нет.