
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 440 Дорофеев, Суворова — Подробные Ответы
Среди данных уравнений найдите уравнения параболы, гиперболы, окружности, прямой:
;
;
;
;
;
;
;
.
Постройте график каждого уравнения.
;
График функции — парабола:
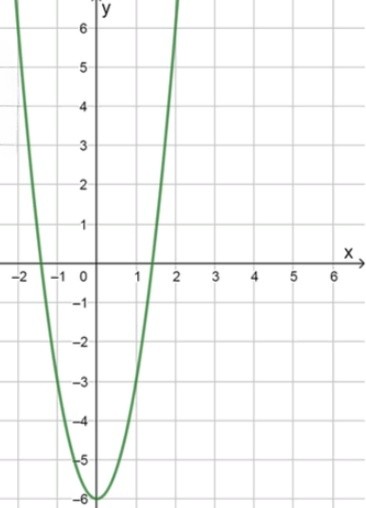
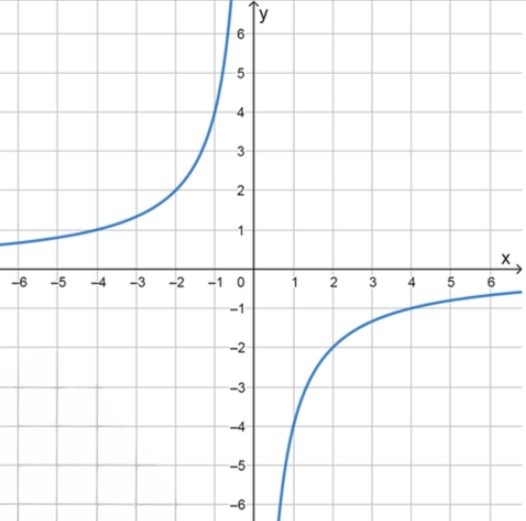
График функции — гипербола:
;
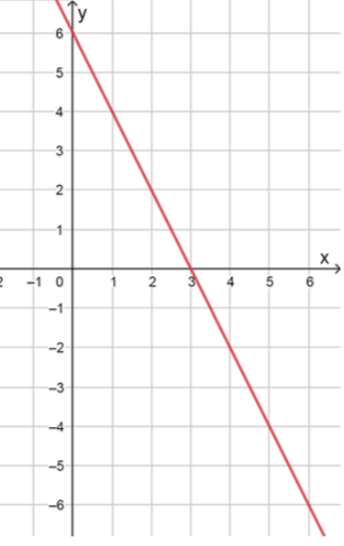
График функции — прямая:
;
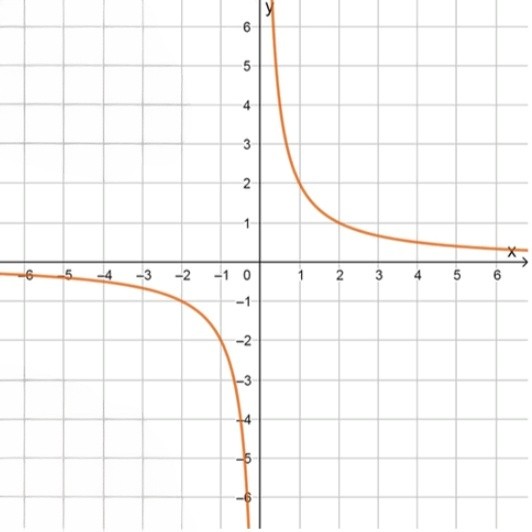
График функции — гипербола:
График функции — окружность:
;
График функции — парабола:
;
График функции — прямая
;
График функции — окружность:
;
Переносим в правую часть: .
Умножаем обе части уравнения на , чтобы избавиться от дроби и получить явный вид функции:
.
Это уравнение параболы, ветви которой направлены вверх (так как при стоит положительный коэффициент ).
Вершина параболы имеет координаты:
, так как парабола не содержит линейного члена.
.
Следовательно, вершина параболы — точка .
;
Выразим в явном виде: .
Это уравнение обратной пропорциональности, график — гипербола.
График расположен в II и IV координатных четвертях, так как произведение переменных даёт отрицательное число.
При , ; при , .
Функция не определена при , так как на ноль делить нельзя.
;
Выразим : .
Это линейная функция с угловым коэффициентом , график — прямая, наклонённая вниз.
Найдём точки для построения:
Если , то ;
Если , то .
Точки: и — достаточно для построения прямой.
;
Переносим вправо: .
Умножим обе части на : .
Разделим на : .
Это снова гипербола, но с положительным значением произведения.
Значит, график будет расположен в I и III координатных четвертях.
Для построения подставим значения :
;
;
;
;
;
;
;
.
Полученные точки отражают гиперболу в I и III четвертях.
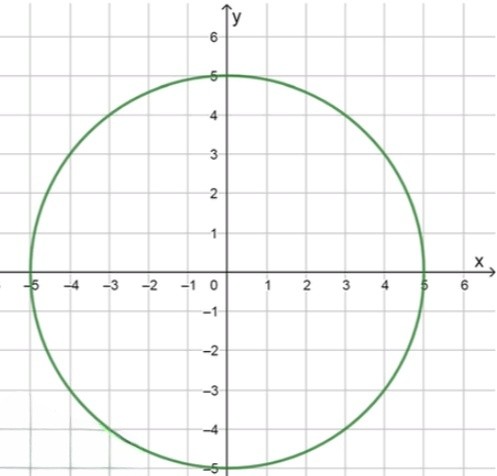
;
Это уравнение окружности с центром в начале координат.
Стандартный вид окружности: , где — центр окружности, — радиус.
Здесь , , .
Центр: , радиус: .
График — окружность, проходящая через точки .
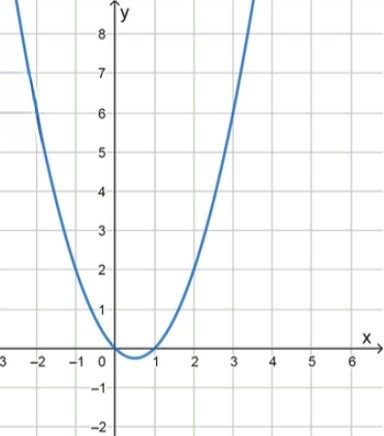
;
Выразим : .
Это уравнение параболы, ветви вверх.
Найдём координаты вершины по формуле:
,
.
Вершина: .
Парабола проходит через начало координат, так как при , .
Также: при , , то есть вершина расположена между этими точками.
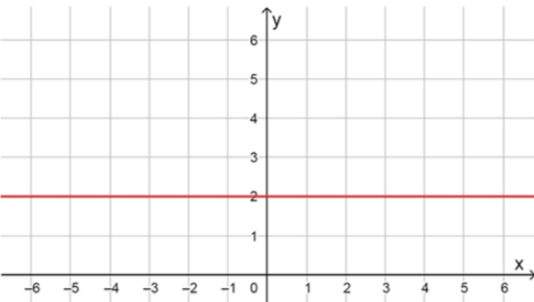
;
Переносим: .
Это уравнение прямой, параллельной оси абсцисс (горизонтальная прямая).
Она проходит через все точки, у которых координата , независимо от значения .
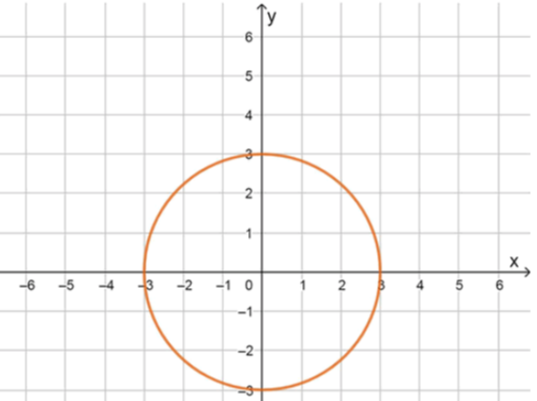
;
Приведём к виду окружности: .
Это окружность с центром в начале координат и радиусом .
Центр окружности: , радиус: .
График проходит через точки .







Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!