ГДЗ Дорофеев 9 Класс по Алгебре Шарыгин Учебник 📕 Суворова- Все Части

ГДЗ по Алгебре 9 Класс Номер 392 Дорофеев, Суворова - Подробные Ответы

Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. и др.

9 класс

Тип

ГДЗ, Решебник.

Автор

Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. и др.

Год

2022.

Издательство

Просвещение.

Описание

Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.

Оцени решение

← Предыдущий Следующий →

Сообщить об ошибке

ГДЗ по Алгебре 9 Класс Номер 392 Дорофеев, Суворова — Подробные Ответы

Задача

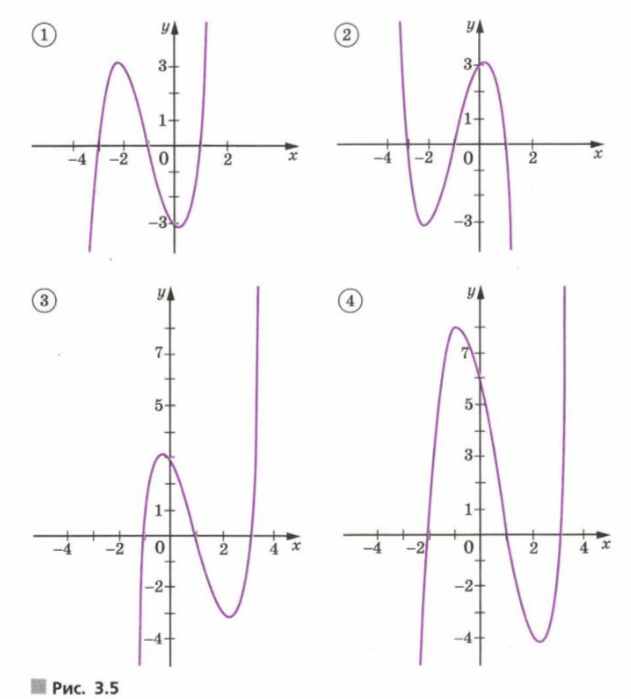
На рисунке 3.5 изображены графики функций:

$f (x) = (x - 1) (x + 1) (x - 3), p (x) = (x - 1) (x + 2) (x - 3),$

$f(x) = (x — 1)(x + 1)(x — 3), \quad p(x) = (x — 1)(x + 2)(x — 3),$ $g(x) = (x + 1)(x — 1)(x + 3), \quad q(x) = -(x + 1)(x — 1)(x + 3).$

Соотнесите каждый график с формулой.

Краткий ответ

$f(x) = (x — 1)(x + 1)(x — 3)$ ;

Нули функции:

$(x — 1)(x + 1)(x — 3) = 0;$

$x — 1 = 0$ , отсюда $x = 1$ ;

$x + 1 = 0$ , отсюда $x = -1$ ;

$x — 3 = 0$ , отсюда $x = 3$ ;

Соответствует графику 3;

$g(x) = (x + 1)(x — 1)(x + 3)$ ;

Нули функции:

$(x + 1)(x — 1)(x + 3) = 0;$

$x + 1 = 0$ , отсюда $x = -1$ ;

$x — 1 = 0$ , отсюда $x = 1$ ;

$x + 3 = 0$ , отсюда $x = -3$ ;

При $x = 0$ принимает значение:

$y = (0 + 1)(0 — 1)(0 + 3) = 1 \cdot (-1) \cdot 3 = -3;$

Соответствует графику 1;

$p(x) = (x — 1)(x + 2)(x — 3)$ ;

Нули функции:

$(x — 1)(x + 2)(x — 3) = 0;$

$x — 1 = 0$ , отсюда $x = 1$ ;

$x + 2 = 0$ , отсюда $x = -2$ ;

$x — 3 = 0$ , отсюда $x = 3$ ;

Соответствует графику 4;

$q(x) = -(x + 1)(x — 1)(x + 3)$ ;

Нули функции:

$-(x + 1)(x — 1)(x + 3) = 0;$

$x + 1 = 0$ , отсюда $x = -1$ ;

$x — 1 = 0$ , отсюда $x = 1$ ;

$x + 3 = 0$ , отсюда $x = -3$ ;

При $x = 0$ принимает значение:

$y = -(0 + 1)(0 — 1)(0 + 3) = -1 \cdot (-1) \cdot 3 = 3;$

Соответствует графику 2.

Подробный ответ

$f(x) = (x — 1)(x + 1)(x — 3)$

Нули функции:

$(x — 1)(x + 1)(x — 3) = 0$

Каждый из множителей равен нулю:

$x — 1 = 0 \quad \Rightarrow \quad x = 1$ $x + 1 = 0 \quad \Rightarrow \quad x = -1$ $x — 3 = 0 \quad \Rightarrow \quad x = 3$

Таким образом, нули функции $f(x)$ — это $x = 1$ , $x = -1$ , $x = 3$ .

Соответствует графику 3.

$g(x) = (x + 1)(x — 1)(x + 3)$

Нули функции:

$(x + 1)(x — 1)(x + 3) = 0$

Каждый из множителей равен нулю:

$x + 1 = 0 \quad \Rightarrow \quad x = -1$ $x — 1 = 0 \quad \Rightarrow \quad x = 1$ $x + 3 = 0 \quad \Rightarrow \quad x = -3$

При $x = 0$ подставим в выражение для $g(x)$ :

$g(0) = (0 + 1)(0 — 1)(0 + 3) = 1 \cdot (-1) \cdot 3 = -3$

Таким образом, нули функции $g(x)$ — это $x = -1$ , $x = 1$ , $x = -3$ , и при $x = 0$ функция принимает значение $-3$ .

Соответствует графику 1.

$p(x) = (x — 1)(x + 2)(x — 3)$

Нули функции:

$(x — 1)(x + 2)(x — 3) = 0$

Каждый из множителей равен нулю:

$x — 1 = 0 \quad \Rightarrow \quad x = 1$ $x + 2 = 0 \quad \Rightarrow \quad x = -2$ $x — 3 = 0 \quad \Rightarrow \quad x = 3$

Таким образом, нули функции $p(x)$ — это $x = 1$ , $x = -2$ , $x = 3$ .

Соответствует графику 4.

$q(x) = -(x + 1)(x — 1)(x + 3)$

Нули функции:

$-(x + 1)(x — 1)(x + 3) = 0$

Каждый из множителей равен нулю:

$x + 1 = 0 \quad \Rightarrow \quad x = -1$ $x — 1 = 0 \quad \Rightarrow \quad x = 1$ $x + 3 = 0 \quad \Rightarrow \quad x = -3$

При $x = 0$ подставим в выражение для $q(x)$ :

$q(0) = -(0 + 1)(0 — 1)(0 + 3) = -1 \cdot (-1) \cdot 3 = 3$

Таким образом, нули функции $q(x)$ — это $x = -1$ , $x = 1$ , $x = -3$ , и при $x = 0$ функция принимает значение $3$ .

Соответствует графику 2.

Оцени решение

← Предыдущий Следующий →

Сообщить об ошибке

Общая оценка

4.2 / 5

Комментарии

Оставь свой отзыв 💬

Комментариев пока нет, будьте первым!

Другие предметы

ГДЗ Дорофеев 7, 8, 9 Класс по Алгебре Все Учебники - Ответы на Любые Задачи Бесплатно

7-9 класс

7 8 9

ГДЗ Дорофеев 1, 2, 3, 4, 5, 6 Класс по Математике Все Учебники - Ответы на Любые Задачи Бесплатно

1-6 класс

1 2 3 4 5 6