ГДЗ по Алгебре 9 Класс Номер 377 Дорофеев, Суворова — Подробные Ответы

а) $y = (\sqrt{x})^2$;

б) $y = \sqrt{x^2}$;

в) $y = (\sqrt{x — 1})^2$.

а) $y = (\sqrt{x})^2 = x$;

1) Функция определена при:
$x \geq 0$;

2) График функции — прямая:

$\begin{array}{c|c|c} x & 0 & 2 \\ \hline y & 0 & 2 \\ \end{array}$

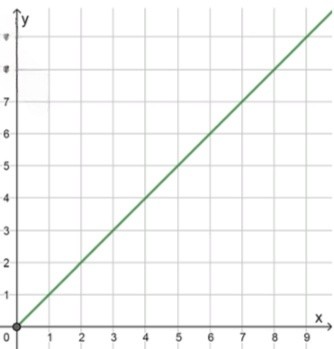
б) $y = \sqrt{x^2} = |x|$;

1) Функция определена при:
$x^2 \geq 0 \quad \text{— верно при любом значении } x$;

2) График функции — модуль:

$\begin{array}{c|c|c|c} x & -1 & 0 & 1 \\ \hline y & 1 & 0 & 1 \\ \end{array}$

в) $y = (\sqrt{x — 1})^2 = x — 1$;

1) Функция определена при:
$x — 1 \geq 0$, отсюда $x \geq 1$;

2) График функции — прямая:

$\begin{array}{ccc}x& 1& 2\\ y& 0& 1\end{array}$

$\begin{array}{c|c|c} x & 1 & 2 \\ \hline y & 0 & 1 \\ \end{array}$

а) $y = (\sqrt{x})^2 = x$

Пояснение: операция возведения в квадрат и извлечение квадратного корня являются взаимно обратными, но только в пределах области определения функции $\sqrt{x}$. Корень определён только при $x \geq 0$, и при этом $\sqrt{x} \geq 0$.

Следовательно, $(\sqrt{x})^2 = x$ только при $x \geq 0$, и функция принимает вид
$y = x$, но определена только для неотрицательных значений аргумента.

Область определения:
$x \geq 0$

Множество значений:
$y \geq 0$

График: правая половина прямой $y = x$, начиная с точки $(0, 0)$

Контрольные точки:
при $x = 0 \Rightarrow y = 0$,
при $x = 2 \Rightarrow y = 2$

Таблица значений:
$\begin{array}{c|c|c} x & 0 & 2 \\ \hline y & 0 & 2 \\ \end{array}$

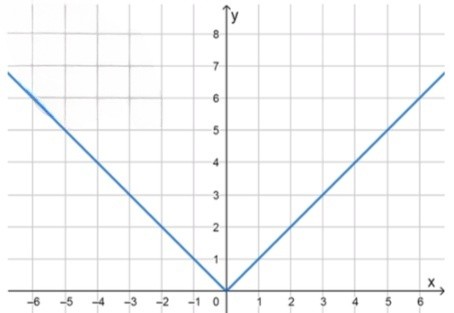
б) $y = \sqrt{x^2} = |x|$

Пояснение: выражение $\sqrt{x^2}$ означает положительное значение выражения $x$, независимо от его знака. Это эквивалентно определению модуля числа.

Для всех действительных $x$ значение $x^2 \geq 0$, и корень определён, так как подкоренное выражение неотрицательно при любом $x$.
Следовательно, $y = \sqrt{x^2} = |x|$, и функция определена на всей числовой прямой.

Область определения:
$x \in \mathbb{R}$

Множество значений:
$y \geq 0$

График: модуль, составленный из двух лучей:
— для $x \geq 0$, график совпадает с прямой $y = x$;
— для $x < 0$, график совпадает с прямой $y = -x$

Контрольные точки:
$x = -1 \Rightarrow y = |-1| = 1$
$x = 0 \Rightarrow y = |0| = 0$
$x = 1 \Rightarrow y = |1| = 1$

Таблица значений:
$\begin{array}{c|c|c|c} x & -1 & 0 & 1 \\ \hline y & 1 & 0 & 1 \\ \end{array}$

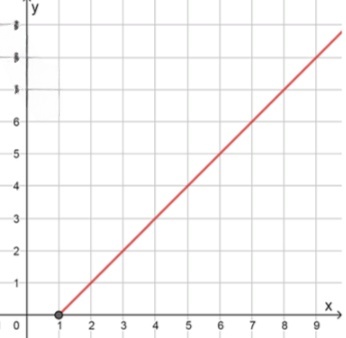
в) $y = (\sqrt{x — 1})^2 = x — 1$

Пояснение: аналогично первому примеру, квадрат и корень взаимно обратны, но только если выражение под корнем $x — 1 \geq 0$.
Следовательно, равенство $(\sqrt{x — 1})^2 = x — 1$ справедливо только при $x \geq 1$

Функция представляет собой линейную зависимость $y = x — 1$, но определена только на полуинтервале $x \geq 1$

Область определения:
$x \geq 1$

Множество значений:
$y \geq 0$

График: луч, начиная с точки $(1, 0)$, продолжается по прямой $y = x — 1$ вправо

Контрольные точки:
при $x = 1 \Rightarrow y = 0$
при $x = 2 \Rightarrow y = 1$

Таблица значений:
$\begin{array}{ccc}x& 1& 2\\ y& 0& 1\end{array}$

$\begin{array}{c|c|c} x & 1 & 2 \\ \hline y & 0 & 1 \\ \end{array}$