Краткий ответ:
а) y = x 2 − 4 x + 2 = ( x − 2 ) ( x + 2 ) x + 2 = x − 2 y = \frac{x^2 — 4}{x + 2} = \frac{(x — 2)(x + 2)}{x + 2} = x — 2
1) Функция определена при:x + 2 ≠ 0 x + 2 \neq 0 x ≠ − 2 x \neq -2
y ≠ − 2 − 2 = − 4 y \neq -2 — 2 = -4
2) График функции — прямая:x 0 2 y − 2 0 \begin{array}{c|c|c} x & 0 & 2 \\ \hline y & -2 & 0 \\ \end{array}
б) y = x − 1 x 2 − x = x − 1 x ( x − 1 ) = 1 x y = \frac{x — 1}{x^2 — x} = \frac{x — 1}{x(x — 1)} = \frac{1}{x}
1) Функция определена при:x ≠ 0 x \neq 0 x − 1 ≠ 0 x — 1 \neq 0 x ≠ 1 x \neq 1
y ≠ 1 1 = 1 y \neq \frac{1}{1} = 1
2) График функции — гипербола:x 0 = 0 x_0 = 0 y 0 = 0 y_0 = 0
x − 2 − 1 − 0.5 0.5 2 y − 0.5 − 1 − 2 2 0.5 \begin{array}{c|c|c|c|c|c} x & -2 & -1 & -0.5 & 0.5 & 2 \\ \hline y & -0.5 & -1 & -2 & 2 & 0.5 \\ \end{array}
в) y = x 2 − 4 x − 5 x + 1 y = \frac{x^2 — 4x — 5}{x + 1}
1) Разложим на множители:x 2 − 4 x − 5 = x 2 + x − 5 x − 5 = x ( x + 1 ) − 5 ( x + 1 ) = ( x − 5 ) ( x + 1 ) x^2 — 4x — 5 = x^2 + x — 5x — 5 = x(x + 1) — 5(x + 1) = (x — 5)(x + 1)
2) Получим функцию:y = ( x − 5 ) ( x + 1 ) x + 1 = x − 5 y = \frac{(x — 5)(x + 1)}{x + 1} = x — 5
3) Функция определена при:x + 1 ≠ 0 x + 1 \neq 0 x ≠ − 1 x \neq -1
y ≠ − 1 − 5 = − 6 y \neq -1 — 5 = -6
4) График функции — прямая:x 0 5 y − 5 0 \begin{array}{c|c|c} x & 0 & 5 \\ \hline y & -5 & 0 \\ \end{array}
г) y = x 4 − 1 x 2 − 1 = ( x 2 − 1 ) ( x 2 + 1 ) x 2 − 1 = x 2 + 1 y = \frac{x^4 — 1}{x^2 — 1} = \frac{(x^2 — 1)(x^2 + 1)}{x^2 — 1} = x^2 + 1
1) Функция определена при:x 2 − 1 ≠ 0 ⇒ x 2 = 1 x^2 — 1 \neq 0 \Rightarrow x^2 = 1 x ≠ ± 1 x \neq \pm 1
y ≠ ( ± 1 ) 2 + 1 = 1 + 1 = 2 y \neq (\pm 1)^2 + 1 = 1 + 1 = 2
2) График функции — парабола:x 0 = 0 x_0 = 0 y 0 = 0 y_0 = 0
x − 3 − 2 2 3 y 10 5 5 10
\begin{array}{c|c|c|c|c} x & -3 & -2 & 2 & 3 \\ \hline y & 10 & 5 & 5 & 10 \\ \end{array}
Подробный ответ:
а) y = x 2 − 4 x + 2 y = \frac{x^2 — 4}{x + 2}
Рассмотрим числитель: x 2 − 4 x^2 — 4 x 2 − 4 = x 2 − 2 2 = ( x − 2 ) ( x + 2 ) x^2 — 4 = x^2 — 2^2 = (x — 2)(x + 2)
Следовательно:y = ( x − 2 ) ( x + 2 ) x + 2 y = \frac{(x — 2)(x + 2)}{x + 2}
Сократим на x + 2 x + 2 x ≠ − 2 x \neq -2 y = x − 2 y = x — 2 x ≠ − 2 x \neq -2
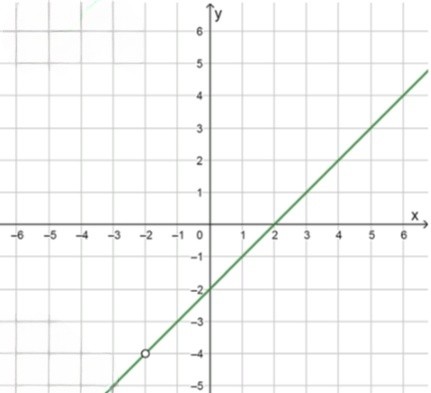
Функция тождественно равна линейной функции y = x − 2 y = x — 2 x = − 2 x = -2
Проверим поведение функции в окрестности x = − 2 x = -2
При x → − 2 − x \rightarrow -2^- y → − 4 y \rightarrow -4 x → − 2 + x \rightarrow -2^+ y → − 4 y \rightarrow -4 x = − 2 x = -2
Значение y = − 4 y = -4 x = − 2 x = -2
Область определения: все x x − 2 -2 x ∈ R ∖ { − 2 } x \in \mathbb{R} \setminus \{ -2 \}
Множество значений: все y y − 4 -4 y ∈ R ∖ { − 4 } y \in \mathbb{R} \setminus \{ -4 \}
График: прямая y = x − 2 y = x — 2 x = − 2 x = -2
Контрольные точки:x = 0 x = 0 y = 0 − 2 = − 2 y = 0 — 2 = -2 x = 2 x = 2 y = 2 − 2 = 0 y = 2 — 2 = 0
Таблица:x 0 2 y − 2 0 \begin{array}{c|c|c} x & 0 & 2 \\ \hline y & -2 & 0 \\ \end{array}
б) y = x − 1 x 2 − x y = \frac{x — 1}{x^2 — x}
Знаменатель: x 2 − x = x ( x − 1 ) x^2 — x = x(x — 1)
Выражение принимает вид:y = x − 1 x ( x − 1 ) y = \frac{x — 1}{x(x — 1)}
Сокращаем на x − 1 x — 1 x ≠ 1 x \neq 1 y = 1 x y = \frac{1}{x} x ≠ 0 x \neq 0 x ≠ 1 x \neq 1
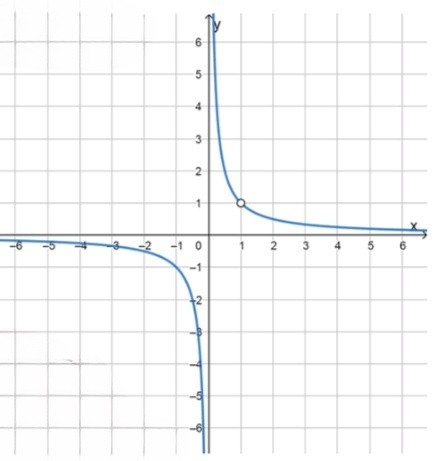
Функция равна y = 1 x y = \frac{1}{x} x = 0 x = 0 x = 1 x = 1
Область определения:x ∈ R ∖ { 0 , 1 } x \in \mathbb{R} \setminus \{ 0, 1 \}
Множество значений:y ∈ R ∖ { 1 } y \in \mathbb{R} \setminus \{ 1 \} x = 1 x = 1 y y
График — гипербола, выколоты точки:x = 0 x = 0 y = 0 y = 0 ( 1 , 1 ) (1, 1)
Контрольные точки:x = − 2 ⇒ y = 1 − 2 = − 0.5 x = -2 \Rightarrow y = \frac{1}{-2} = -0.5 x = − 1 ⇒ y = 1 − 1 = − 1 x = -1 \Rightarrow y = \frac{1}{-1} = -1 x = − 0.5 ⇒ y = 1 − 0.5 = − 2 x = -0.5 \Rightarrow y = \frac{1}{-0.5} = -2 x = 0.5 ⇒ y = 1 0.5 = 2 x = 0.5 \Rightarrow y = \frac{1}{0.5} = 2 x = 2 ⇒ y = 1 2 = 0.5 x = 2 \Rightarrow y = \frac{1}{2} = 0.5
Таблица:x − 2 − 1 − 0.5 0.5 2 y − 0.5 − 1 − 2 2 0.5 \begin{array}{c|c|c|c|c|c} x & -2 & -1 & -0.5 & 0.5 & 2 \\ \hline y & -0.5 & -1 & -2 & 2 & 0.5 \\ \end{array}
в) y = x 2 − 4 x − 5 x + 1 y = \frac{x^2 — 4x — 5}{x + 1}
Разложим числитель:x 2 − 4 x − 5 = x 2 + x − 5 x − 5 = x ( x + 1 ) − 5 ( x + 1 ) = ( x + 1 ) ( x − 5 ) x^2 — 4x — 5 = x^2 + x — 5x — 5 = x(x + 1) — 5(x + 1) = (x + 1)(x — 5)
Получаем:y = ( x + 1 ) ( x − 5 ) x + 1 y = \frac{(x + 1)(x — 5)}{x + 1}
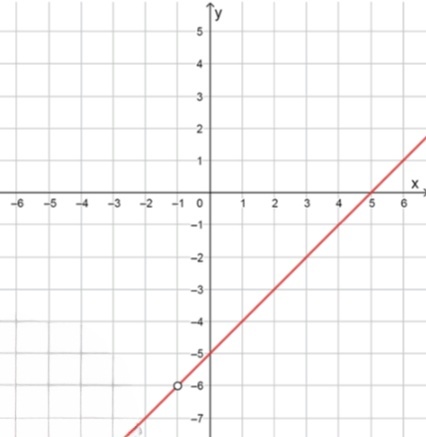
Сократим на x + 1 x + 1 x ≠ − 1 x \neq -1 y = x − 5 y = x — 5 x ≠ − 1 x \neq -1
Функция определена всюду, кроме x = − 1 x = -1
Область определения:x ∈ R ∖ { − 1 } x \in \mathbb{R} \setminus \{ -1 \}
Множество значений:y ∈ R ∖ { − 6 } y \in \mathbb{R} \setminus \{ -6 \} x = − 1 x = -1 y = − 6 y = -6
График — прямая y = x − 5 y = x — 5 x = − 1 x = -1
Контрольные точки:x = 0 ⇒ y = 0 − 5 = − 5 x = 0 \Rightarrow y = 0 — 5 = -5 x = 5 ⇒ y = 5 − 5 = 0 x = 5 \Rightarrow y = 5 — 5 = 0
Таблица:x 0 5 y − 5 0 \begin{array}{c|c|c} x & 0 & 5 \\ \hline y & -5 & 0 \\ \end{array}
г) y = x 4 − 1 x 2 − 1 y = \frac{x^4 — 1}{x^2 — 1}
Разложим числитель:x 4 − 1 = ( x 2 ) 2 − 1 2 = ( x 2 − 1 ) ( x 2 + 1 ) x^4 — 1 = (x^2)^2 — 1^2 = (x^2 — 1)(x^2 + 1)
Получаем:y = ( x 2 − 1 ) ( x 2 + 1 ) x 2 − 1 y = \frac{(x^2 — 1)(x^2 + 1)}{x^2 — 1}
Сокращаем на x 2 − 1 x^2 — 1 x 2 ≠ 1 ⇒ x ≠ ± 1 x^2 \neq 1 \Rightarrow x \neq \pm 1
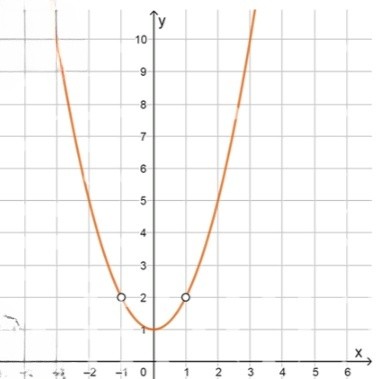
Получаем:y = x 2 + 1 y = x^2 + 1 x ≠ ± 1 x \neq \pm 1
Область определения:x ∈ R ∖ { − 1 , 1 } x \in \mathbb{R} \setminus \{ -1, 1 \}
Множество значений:y ∈ ( 1 , + ∞ ) ∖ { 2 } y \in (1, +\infty) \setminus \{ 2 \} x = ± 1 ⇒ y = 2 x = \pm 1 \Rightarrow y = 2
График — парабола y = x 2 + 1 y = x^2 + 1 x = ± 1 x = \pm 1
Контрольные точки:x = − 3 ⇒ y = 9 + 1 = 10 x = -3 \Rightarrow y = 9 + 1 = 10 x = − 2 ⇒ y = 4 + 1 = 5 x = -2 \Rightarrow y = 4 + 1 = 5 x = 2 ⇒ y = 4 + 1 = 5 x = 2 \Rightarrow y = 4 + 1 = 5 x = 3 ⇒ y = 9 + 1 = 10 x = 3 \Rightarrow y = 9 + 1 = 10
Таблица:x − 3 − 2 2 3 y 10 5 5 10
\begin{array}{c|c|c|c|c} x & -3 & -2 & 2 & 3 \\ \hline y & 10 & 5 & 5 & 10 \\ \end{array}





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!